
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Рентгеновский структурный анализ | Рентгеновский структурный анализ (далее Р) методы исследования структуры вещества по распределению в пространстве и интенсивностям рассеянного на анализируемом объекте рентгеновского излучения. Р наряду с нейтронографией и электронографией является дифракционным структурным методом; в его основе лежит взаимодействие рентгеновского излучения с электронами вещества, в результате которого возникает дифракция рентгеновских лучей. Дифракционная картина зависит от длины волны используемых рентгеновских лучей и строения объекта. Для исследования структуры применяют излучение с длиной волны ~1 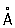 , т. е. порядка размеров Методами Р изучают металлы, сплавы, минералы, неорганические и органические соединения, полимеры, аморфные материалы, жидкости и газы, молекулы нуклеиновых кислот и т.д. Наиболее успешно Р применяют для установления структуры тел. Это обусловлено тем, что кристаллы обладают строгой периодичностью строения и представляют собой созданную самой природой дифракционную решетку для рентгеновских лучей. , т. е. порядка размеров Методами Р изучают металлы, сплавы, минералы, неорганические и органические соединения, полимеры, аморфные материалы, жидкости и газы, молекулы нуклеиновых кислот и т.д. Наиболее успешно Р применяют для установления структуры тел. Это обусловлено тем, что кристаллы обладают строгой периодичностью строения и представляют собой созданную самой природой дифракционную решетку для рентгеновских лучей.
Историческая справка. Дифракция рентгеновских лучей на была открыта в 1912 немецкими физиками М. Лауэ, В. Фридрихом и П. Книппингом. Направив узкий пучок рентгеновских лучей на неподвижный они зарегистрировали на помещенной за фотопластинке дифракционную картину, которая состояла из большого числа закономерно расположенных пятен. Каждое пятно — след дифракционного луча, рассеянного Рентгенограмма, полученная таким методом, носит название лауэграммы (рис. 1).
Разработанная Лауэ теория дифракции рентгеновских лучей на позволила связать длину волны l излучения, параметры элементарной ячейки а, b, с (см. Кристаллическая решетка), углы падающего (a0, b0, g0) и дифракционного (a, b, g) лучей соотношениями:
a (cosa— cosa0) = hl,
b (cosb — cosb0) = kl, (1)
c (cosg — cosg0) =ll,
где h, k, — целые числа (миллеровские индексы). Для возникновения дифракционного луча необходимо выполнение приведенных условий Лауэ (уравнений (1)), которые требуют, чтобы в параллельных лучах разность хода между лучами, рассеянными отвечающими соседним узлам решетки, были равны целому числу длин волн.
В 1913 У. Л. Брэгг и одновременно с ним Г. В. Вульф предложили более наглядную трактовку возникновения дифракционных лучей в Они показали, что любой из дифракционных лучей можно рассматривать как отражение падающего луча от одной из систем плоскостей (дифракционное отражение, см. Брэгга — Вульфа условие). В том же году У. Г. и У. Л. Брэгги впервые исследовали структуры простейших с помощью рентгеновских дифракционных методов. В 1916 П. Дебай и немецкий физик П. Шеррер предложили использовать дифракцию рентгеновских лучей для исследования структуры поликристаллических материалов. В 1938 французский А. Гинье разработал метод рентгеновского малоуглового рассеяния для исследования формы и размеров неоднородностей в веществе.
Применимость Р к исследованию широкого класса веществ, производственная необходимость этих исследований стимулировали развитие методов расшифровки структур. В 1934 американский физик А. Патерсон предложил исследовать строение веществ с помощью функции межатомных векторов (функции Патерсона). Американские ученые Д. Харкер, Дж. Каспер (1948), У. Захариасен, Д. Сейр и английский ученый В. Кокрен (1952) заложили основы так называемых прямых методов определения структур. Большой вклад в развитие патерсоновских и прямых методов Р внесли Н. В. Белов, Г. С. Жданов, А. И. Китайгородский, Б. К. Вайнштейн, М. Порай-Кошиц (СССР), Л. Полинг, П. Эвальд, М. Бюргер, Дж. Карле, Г. Хауптман (США), М. Вульфсон (Великобритания) и др. Работы по исследованию пространственной структуры начатые в Англии Дж. Берналом (30-е гг.) и успешно продолженные Дж. Кендрю, М. Перуцем, Д. Кроуфут-Ходжкин и др., сыграли исключительно важную роль в становлении молекулярной биологии. В 1953 Дж. Уотсон и Ф. Крик предложили модель молекулы дезоксирибонуклеиновой кислоты (ДНК), которая хорошо согласовалась с результатами рентгенографических исследований ДНК, полученными М. Уилкинсом.
В 50-х гг. начали бурно развиваться методы Р с использованием ЭВМ в технике эксперимента и при обработке рентгеновской дифракционной информации.
Экспериментальные методы Р Для создания условий дифракции и регистрации излучения служат рентгеновские камеры и рентгеновские дифрактометры. Рассеянное рентгеновское излучение в них фиксируется на фотопленке или измеряется детекторами ядерных излучений. В зависимости от состояния исследуемого образца и его свойств, а также от характера и объема информации, которую необходимо получить, применяют различные методы Р Монокристаллы, отбираемые для исследования структуры, должны иметь размеры ~ 0,1 мм и по возможности обладать совершенной структурой. Исследованием дефектов в сравнительно крупных почти совершенных занимается рентгеновская топография, которую иногда относят к Р
Метод Лауэ — простейший метод получения рентгенограмм от монокристаллов. в эксперименте Лауэ неподвижен, а используемое рентгеновское излучение имеет непрерывный спектр. Расположение дифракционных пятен на лауэграммах (рис. 1) зависит от симметрии кристалла и его ориентации относительно падающего луча. Метод Лауэ позволяет установить принадлежность исследуемого к одной и 11 лауэвских групп симметрии и ориентировать его (т. е. определять направление осей) с точностью до нескольких угловых минут. По характеру пятен на лауэграммах и особенно появлению астеризма можно выявить внутренние напряжения и некоторые др. дефекты структуры. Методом Лауэ проверяют качество монокристаллов при выборе образца для его более полного структурного исследования.
Методы качания и вращения образца используют для определения периодов повторяемости (постоянной решетки) вдоль направления в монокристалле. Они позволяют, в частности, установить параметры а, b, с элементарной ячейки В этом методе используют монохроматическое рентгеновское излучение, образец приводится в колебательное или вращательное движение вокруг оси, совпадающей с направлением, вдоль которого и исследуют период повторяемости. Пятна на рентгенограммах качания и вращения, полученных в цилиндрических кассетах, располагаются на семействе параллельных линий. Расстояния между этими линиями, длина волны излучения и диаметр кассеты рентгеновской камеры позволяют вычислить искомый период повторяемости в Условия Лауэ для дифракционных лучей в этом методе выполняются за счет изменения углов, входящих в соотношения (1) при качании или вращении образца.
Рентгенгониометрические методы. Для полного исследования структуры монокристалла методами Р необходимо не только установить положение, но и измерить интенсивности как можно большего числа дифракционных отражений, которые могут быть получены от при данной длине волны излучения и всех возможных ориентациях образца. Для этого дифракционную картину регистрируют на фотопленке в рентгеновском гониометре и измеряют с помощью микрофотометра степень почернения каждого пятна на рентгенограмме. В рентгеновском дифрактометре можно непосредственно измерять интенсивность дифракционных отражений с помощью пропорциональных, сцинтилляционных и других счетчиков рентгеновских квантов. Чтобы иметь полный набор отражений, в рентгеновских гониометрах получают серию рентгенограмм. На каждой из них фиксируются дифракционные отражения, на миллеровские индексы которых накладывают определенные ограничения (например, на разных рентгенограммах регистрируются отражения типа hk0, hk1 и т.д.). Наиболее часто производят рентгеногониометрический эксперимент по методам Вайсенберга. Бюргера (рис. 2) и де Ионга — Боумена. Такую же информацию можно получить и с помощью рентгенограмм качания.
Для установления структуры средней сложности (~ 50—100 в элементарной ячейке) необходимо измерить интенсивности нескольких сотен и даже тысяч дифракционных отражений. Эту весьма трудоемкую и кропотливую работу выполняют автоматические микроденситометры и дифрактометры, управляемые ЭВМ, иногда в течение нескольких недель и даже месяцев (например, при анализе структур когда число отражений возрастает до сотен тысяч). Применением в дифрактометре нескольких счетчиков, которые могут параллельно регистрировать отражения, время эксперимента удается значительно сократить. Дифрактометрические измерения превосходят фоторегистрацию по чувствительности и точности.
Метод исследования поликристаллов (Дебая — Шеррера метод). Металлы, сплавы, порошки состоят из множества мелких монокристаллов данного вещества. Для их исследования используют монохроматическое излучение. Рентгенограмма (дебаеграмма) поликристаллов представляет собой несколько концентрических колец, в каждое из которых сливаются отражения от определенной системы плоскостей различно ориентированных монокристаллов. Дебаеграммы различных веществ имеют индивидуальный характер и широко используются для идентификации соединений (в том числе и в смесях). Р.с.а. поликристаллов позволяет определять фазовый состав образцов, устанавливать размеры и преимущественную ориентацию (текстурирование) зерен в веществе, осуществлять контроль за напряжениями в образце и решать другие технические задачи.
Исследование аморфных материалов и частично упорядоченных объектов. Четкую рентгенограмму с острыми дифракционными максимумами можно получить только при полной трехмерной периодичности образца. Чем ниже степень упорядоченности строения материала, тем более размытый, диффузный характер имеет рассеянное им рентгеновское излучение. Диаметр диффузного кольца на рентгенограмме аморфного вещества может служить для грубой оценки средних межатомных расстояний в нем. С ростом степени упорядоченности (см. Дальний порядок и ближний порядок) в строении объектов дифракционная картина усложняется и, следовательно, содержит больше структурной информации.
Метод малоуглового рассеяния позволяет изучать пространственные неоднородности вещества, размеры которых превышают межатомные расстояния, т.е. составляют от 5—10 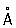 до ~ 10 000 до ~ 10 000 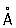 . Рассеянное рентгеновское излучение в этом случае концентрируется вблизи первичного пучка — в области малых углов рассеяния. Малоугловое рассеяние применяют для исследования пористых и мелкодисперсных материалов, сплавов и сложных биологических объектов: вирусов, клеточных мембран, Для изолированных молекул и нуклеиновых кислот метод позволяет определить их форму, размеры, молекулярную массу; в вирусах — характер взаимной укладки составляющих их компонент: нуклеиновых кислот, липидов; в синтетических полимерах — упаковку полимерных цепей; в порошках и сорбентах — распределение частиц и пор по размерам; в сплавах — возникновение и размеры фаз; в текстурах (в частности, в жидких — форму упаковки частиц (молекул) в различного рода надмолекулярные структуры. Рентгеновский малоугловой метод применяется и в промышленности при контроле процессов изготовления катализаторов, высокодисперсных углей и т.д. В зависимости от строения объекта измерения производят для углов рассеяния от долей минуты до нескольких градусов. . Рассеянное рентгеновское излучение в этом случае концентрируется вблизи первичного пучка — в области малых углов рассеяния. Малоугловое рассеяние применяют для исследования пористых и мелкодисперсных материалов, сплавов и сложных биологических объектов: вирусов, клеточных мембран, Для изолированных молекул и нуклеиновых кислот метод позволяет определить их форму, размеры, молекулярную массу; в вирусах — характер взаимной укладки составляющих их компонент: нуклеиновых кислот, липидов; в синтетических полимерах — упаковку полимерных цепей; в порошках и сорбентах — распределение частиц и пор по размерам; в сплавах — возникновение и размеры фаз; в текстурах (в частности, в жидких — форму упаковки частиц (молекул) в различного рода надмолекулярные структуры. Рентгеновский малоугловой метод применяется и в промышленности при контроле процессов изготовления катализаторов, высокодисперсных углей и т.д. В зависимости от строения объекта измерения производят для углов рассеяния от долей минуты до нескольких градусов.
Определение структуры по данным дифракции рентгеновских лучей. Расшифровка структуры включает: установление размеров и формы его элементарной ячейки; определение принадлежности к одной из 230 федоровских (открытых Е. С. Федоровым) групп симметрии кристаллов; получение координат базисных структуры. Первую и частично вторую задачи можно решить методами Лауэ и качания или вращения Окончательно установить группу симметрии и координаты базисных сложных структур возможно только с помощью сложного анализа и трудоемкой математической обработки значений интенсивностей всех дифракционных отражений от данного Конечная цель такой обработки состоит в вычислении по экспериментальным данным значений электронной плотности r(х, у, z) в любой точке ячейки с координатами x, у, z. Периодичность строения позволяет записать электронную плотность в нем через Фурье ряд:
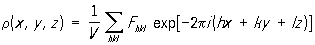 , (2) , (2)
где — объем элементарной ячейки, hkl — коэффициенты Фурье, которые в Р называются структурными амплитудами, i = 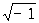 . Каждая структурная амплитуда характеризуется тремя целыми числами hkl и связана с тем дифракционным отражением, которое определяется условиями (1). Назначение суммирования (2) — математически собрать дифракционные рентгеновские отражения, чтобы получить изображение структуры. Производить таким образом синтез изображения в Р приходится из-за отсутствия в природе линз для рентгеновского излучения (в оптике видимого света для этого служит собирающая линза). . Каждая структурная амплитуда характеризуется тремя целыми числами hkl и связана с тем дифракционным отражением, которое определяется условиями (1). Назначение суммирования (2) — математически собрать дифракционные рентгеновские отражения, чтобы получить изображение структуры. Производить таким образом синтез изображения в Р приходится из-за отсутствия в природе линз для рентгеновского излучения (в оптике видимого света для этого служит собирающая линза).
Дифракционное отражение — волновой процесс. Он характеризуется амплитудой, равной ½hkl½, и фазой ahkl (сдвигом фазы отраженной волны по отношению к падающей), через которую выражается структурная амплитуда: hkl =½hkl ½(cosahkl + isinahkl). Дифракционный эксперимент позволяет измерять только интенсивности отражений, пропорциональные ½hkl½2, но не их фазы. Определение фаз составляет основную проблему расшифровки структуры Определение фаз структурных амплитуд в принципиальном отношении одинаково как для состоящих из так и для состоящих из молекул. Определив координаты в молекулярном веществе, можно выделить составляющие его молекулы и установить их размер и форму.
Легко решается задача, обратная структурной расшифровке: вычисление по известной структуре структурных амплитуд, а по ним — интенсивностей дифракционных отражений. Метод проб и ошибок, исторически первый метод расшифровки структур, состоит в сопоставлении экспериментально полученных ½hkl½эксп, с вычисленными на основе пробной модели значениями ½hkl½выч. В зависимости от величины фактора расходимости
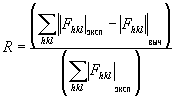
пробная модель принимается или отвергается. В 30-х гг. были разработаны для структур более формальные методы, но для некристаллических объектов метод проб и ошибок по-прежнему является практически единственным средством интерпретации дифракционной картины.
Принципиально новый путь к расшифровке структур монокристаллов открыло применение т. н. функций Патерсона (функций межатомных векторов). Для построения функции Патерсона некоторой структуры, состоящей из перенесем ее параллельно самой себе так, чтобы в фиксированное начало координат попал сначала первый Векторы от начала координат до всех структуры (включая вектор нулевой длины до первого укажут положение максимумов функции межатомных векторов, совокупность которых называется изображением структуры в 1. Добавим к ним еще максимумов, положение которых укажет векторов от второго помещенного при параллельном переносе структуры в то же начало координат. Проделав эту процедуру со всеми (рис. 3), мы получим 2 векторов. Функция, описывающая их положение, и есть функция Патерсона.
Для функции Патерсона Р (u, u, w) (u, u, w — координаты точек в пространстве межатомных векторов) можно получить выражение:
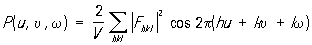 , ,
из которого следует, что она определяется модулями структурных амплитуд, не зависит от их фаз и, следовательно, может быть вычислена непосредственно по данным дифракционного эксперимента. Трудность интерпретации функции Р (u, u, w) состоит в необходимости нахождения координат из 2 ее максимумов, многие из которых сливаются из-за перекрытий, возникающих при построении функции межатомных векторов. Наиболее прост для расшифровки Р (u, u, w) случай, когда в структуре содержится один тяжелый и несколько легких. Изображение такой структуры в тяжелом будет значительно отличаться от др. ее изображений. Среди различных методик, позволяющих определить модель исследуемой структуры по функции Патерсона, наиболее эффективными оказались так называемые суперпозиционные методы, которые позволили формализовать ее анализ и выполнять его на ЭВМ.
Методы функции Патерсона сталкиваются с серьезными трудностями при исследовании структур состоящих из одинаковых пли близких по номеру В этом случае более эффективными оказались Так называемые прямые методы определения фаз структурных амплитуд. Учитывая тот факт, что значение электронной плотности в всегда положительно (или равно нулю), можно получить большое число неравенств, которым подчиняются коэффициенты Фурье (структурные амплитуды) функции r(x, у, z). Методами неравенств можно сравнительно просто анализировать структуры, содержащие до 20—40 в элементарной ячейке Для более сложных структур применяются методы, основанные на вероятностном подходе к проблеме: структурные амплитуды и их фазы рассматриваются как случайные величины; из физических представлений выводятся функции распределения этих случайных величин, которые дают возможность оценить с учетом экспериментальных значений модулей структурных амплитуд наиболее вероятные значения фаз. Эти методы также реализованы на ЭВМ и позволяют расшифровать структуры, содержащие 100—200 и более в элементарной ячейке
Итак, если фазы структурных амплитуд установлены, то по (2) может быть вычислено распределение электронной плотности в максимумы этого распределения соответствуют положению в структуре (рис. 4). Заключительное уточнение координат проводится на ЭВМ наименьших квадратов методом и в зависимости от качества эксперимента и сложности структуры позволяет получить их с точностью до тысячных долей 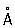 (с помощью современного дифракционного эксперимента можно вычислять также количественные характеристики тепловых колебаний в с учетом анизотропии этих колебаний). Р дает возможность установить и более тонкие характеристики структур, например распределение валентных электронов в Однако эта сложная задача решена пока только для простейших структур. Весьма перспективно для этой цели сочетание нейтронографических и рентгенографических исследований: нейтронографические данные о координатах ядер сопоставляют с распределением в пространстве электронного облака, полученным с помощью Р Для решения многих физических и задач совместно используют рентгеноструктурные исследования и резонансные методы. (с помощью современного дифракционного эксперимента можно вычислять также количественные характеристики тепловых колебаний в с учетом анизотропии этих колебаний). Р дает возможность установить и более тонкие характеристики структур, например распределение валентных электронов в Однако эта сложная задача решена пока только для простейших структур. Весьма перспективно для этой цели сочетание нейтронографических и рентгенографических исследований: нейтронографические данные о координатах ядер сопоставляют с распределением в пространстве электронного облака, полученным с помощью Р Для решения многих физических и задач совместно используют рентгеноструктурные исследования и резонансные методы.
Вершина достижений Р — расшифровка трехмерной структуры нуклеиновых кислот и других макромолекул. в естественных условиях, как правило, не образуют. Чтобы добиться регулярного расположения молекул, и затем исследуют их структуру. Фазы структурных амплитуд можно определить только в результате совместных усилий рентгенографов и биохимиков. Для решения этой проблемы необходимо получить и исследовать самого а также его производных с включением тяжелых причем координаты во всех этих структурах должны совпадать.
О многочисленных применениях методов Р для исследования различных нарушений структуры твердых тел под влиянием всевозможных воздействий см. в ст. Рентгенография материалов.
Лит.: Белов Н. В., Структурная М., 1951; Жданов Г. С., Основы рентгеноструктурного анализа, М. — Л., 1940; Джеймс Р., Оптические принципы дифракции рентгеновских лучей, пер. с англ., М., 1950; Бокий Г. Б., Порай-Кошиц М. А., Рентгеноструктурный анализ, М., 1964; Порай-Кошиц М. А., Практический курс рентгеноструктурного анализа, М., 1960: Китайгородский А. И., Теория структурного анализа, М., 1957; Липеон Г., Кокрен В., Определение структуры пер. с англ., М., 1961; Вайнштейн Б. К., Структурная электронография, М., 1956; Бэкон Дж., Дифракция нейтронов, пер. с англ., М., 1957; Бюргер М., Структура и векторное пространство, пер. с англ., М., 1961; Гинье А., Рентгенография пер. с франц., М., 1961; Woolfson М. М., An introduction to X-ray crystallography, Camb., 1970: Ramachandran G. ., Srinivasan R., Fourier methode in crystallography, . ., 1970; Crystallographic computing, ed. . R. Ahmed, Cph., 1970; Stout G. ., Jensen L. ., X-ray structure determination, . . — L., (1968).
В. И. Симонов.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 27.07.2024 08:46:24
|

|

|
 |
|

|
 |
 |
 |
|