|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Математическое ожидание | Математическое ожидание (далее М), среднее значение, одна из важнейших характеристик распределения вероятностей случайной величины. Для случайной величины X, принимающей последовательность значений y1, y2, ..., yk, ... с вероятностями, равными соответственно p1, p2, ..., pk, …, М определяется формулой
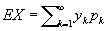
(в предположении, что ряд 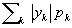 сходится). Так, например, если Х - число очков, выпадающее на верхней грани игральной кости (X принимает каждое из значений 1, 2, 3, 4, 5, 6 с вероятностью 1/6), то  .
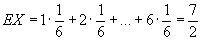Для случайной величины, имеющей плотность вероятности р(у), М определяется формулой
 .
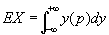М характеризует расположение значений случайной величины. Полностью эта роль М разъясняется больших чисел законом. При сложении случайных величин их М складываются, при умножении двух независимых случайных величин их М перемножаются. М случайной величины eitX, то есть f (t) = Eeitxz, где t - действительное число, носит название характеристической функции.
Лит.: Гнеденко Б. В., Курс теории вероятностей, 4 изд., М., 1965.
Ю. В. Прохоров. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 31.10.2025 17:44:10
|
|
|
|
|
|
|
|
|
|
|
