
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Случайная величина | Случайная величина (далее С) в теории вероятностей, величина, принимающая в зависимости от случая те или иные значения с определенными вероятностями. Так, число очков, выпадающее на верхней грани игральной кости, представляет собой С, принимающую значения 1, 2, 3, 4, 5, 6 с вероятностью 1/6 каждое. Если С Х принимает конечную или бесконечную последовательность различных значений, то ее распределение вероятностей (закон распределения) задается указанием этих значений:
x1, x2,..., xn,...
и соответствующих им вероятностей:
p1, p2,..., pn....
С указанного типа называются дискретными. В других случаях распределение вероятностей задается указанием для каждого отрезка D = (а, b) вероятности Рх (а, b) неравенства а £ х < b. Особенно часто встречаются С, для которых существует такая функция px (x) (плотность вероятности), что
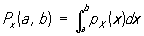
С этого типа называются непрерывными.
Ряд общих свойств распределения вероятностей С достаточно полно описывается небольшим количеством числовых характеристик. Наиболее употребительными среди этих последних являются математическое ожидание ЕХ С Х и ее дисперсия DX. Менее употребительны медиана, мода, квантили и т. п. См. также Вероятностей теория.
Лит.: Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969; Крамер Г., Случайные величины и распределения вероятностей, пер. с англ., М., 1947. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 30.01.2026 10:25:14
|

|

|
 |
|

|
 |
 |
 |
|