
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Характеристическая функция | Характеристическая функция (далее Х)в математике,
1) то же, что собственная функция.
2) Характеристическая функция множества А (в современной терминологии - индикатор А) - функция f (x), определенная на некотором множестве Е, содержащем множество А, и принимающая значение f (x) = 1, если x принадлежит множеству А, и значение f (x) = 0, если x не принадлежит ему. 3) В теории вероятностей Характеристическая функция fX (t) случайной величины Х определяется как математическое ожидание величины eitX. Это определение для случайных величин, имеющих плотность вероятности pX (x), приводит к формуле
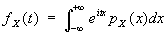 . .
Например, для случайной величины, имеющей нормальное распределение с параметрами а и s, Характеристическая функция равна
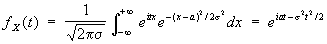 . .
Свойства Характеристическая функция: каждой случайной величине Х соответствует определенная Характеристическая функция fX (t); распределение вероятностей для Х однозначно определяется по fX (t); при сложении независимых случайных величин соответствующие Характеристическая функция перемножаются; при надлежащем определении понятия "близости" случайным величинам с близкими распределениями соответствуют Характеристическая функция, мало отличающиеся друг от друга, и, обратно, близким Характеристическая функция соответствуют случайные величины с близкими распределениями. Указанные свойства лежат в основе применений Характеристическая функция, в частности к выводу предельных теорем теории вероятностей. Впервые аппарат, по существу равнозначный Характеристическая функция, был использован П. Лапласом (1812), но вся сила метода Характеристическая функция была показана А. М. Ляпуновым (1901), получившим с его помощью свою известную теорему.
Понятие Характеристическая функция может быть обобщено на конечные и бесконечные системы случайных величин (т. е. на случайные векторы и случайные процессы).
Теория Характеристическая функция имеет много общего с теорией Фурье интеграла.
Лит.: Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969; Прохоров Ю. В., Розанов Ю. А., Теория вероятностей, 2 изд., М., 1973.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 30.01.2026 10:23:58
|

|

|
 |
|

|
 |
 |
 |
|