|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Якобиан | Якобиан (далее Я), функциональный определитель ½aik½1n с элементами 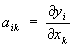 , где yi = fi (X1,..., Xn), l £ i £ n, — функции, имеющие непрерывные частные производные в некоторой области А; обозначение:
 .
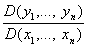Введен К. Якоби (1833, 1841). Если, например, n = 2, то система функций
y1 = f1 (. x1, x2), y2 = f2 (x1, x2) (1)
задает отображение области D, лежащей на плоскости x1, x2, на часть плоскости y1, y2. Роль Я для этого отображения во многом аналогична роли производной для функции одной переменной. Например, абсолютное значение Я в некоторой точке М равно коэффициенту искажения площадей в этой точке (т. е. пределу отношения площади образа окрестности точки М к площади самой окрестности, когда размеры окрестности стремятся к нулю). Я в точке М положителен, если отображение (1) не меняет ориентации в окрестности точки М, и отрицателен в противоположном случае. Если Я не обращается в нуль в области D и j (y1, у2) — функция, заданная в области D1 (образе D), то
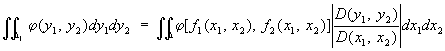
(формула замены переменных в двойном интеграле). Аналогичная формула имеет место для кратных интегралов. Если Я отображения (1) не обращается в нуль в области Д, то существует обратное отображение
x1 = j1 (y1, y2), x1 = j2(y1, y2),
причем
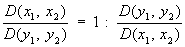
(аналог формулы дифференцирования обратной функции). Это утверждение находит многочисленные применения в теории неявных функций. Для возможности явного выражения в окрестности точки М (x1(0),..., xn (0, y1(0),..., ym (0)) функций y1,..., ут, неявно заданных уравнениями k (x1,..., xn, y1,..., ум) = 0, (2)
1 £ k £ m,
достаточно, чтобы координаты точки М удовлетворяли уравнениям (2), функции Fk имели непрерывные частные производные и Я
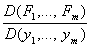
был отличен от нуля в точке М.
Лит.: Кудрявцев Л. Д., Математический анализ, 2 изд., т. 2, М., 1973; Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
