
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Корреляционный анализ | Корреляционный анализ (далее К) совокупность основанных на математической теории корреляции методов обнаружения корреляционной зависимости между двумя случайными признаками или факторами. К экспериментальных данных заключает в себе следующие основные практические приемы: 1) построение корреляционного поля и составление корреляционной таблицы; 2) вычисление выборочных коэффициентов корреляции или корреляционного отношения; 3) проверка статистической гипотезы значимости связи. Дальнейшее исследование заключается в установлении конкретного вида зависимости между величинами (см. Регрессионный анализ). Зависимость между тремя и большим числом случайных признаков или факторов изучается методами многомерного К (вычисление частных и множественных коэффициентов корреляции и корреляционных отношений).
Корреляционное поле и корреляционная таблица являются вспомогательными средствами при анализе выборочных данных. При нанесении на координатную плоскость выборочных точек получают корреляционное поле. По характеру расположения точек поля можно составить предварительное мнение о форме зависимости случайных величин (например, о том, что одна величина в среднем возрастает или убывает при возрастании другой). Для численной обработки результаты обычно группируют и представляют в форме корреляционной таблицы. В каждой клетке корреляционной таблицы (см. в ст. Корреляция в математической статистике) приводятся численности гц; тех пар (х, у), компоненты которых попадают в соответствующие интервалы группировки по каждой переменной.
Предполагая длины интервалов группировки (по каждому из переменных) равными между собой, выбирают центры xi (соответственно yj) этих интервалов и числа nij в качестве основы для расчетов.
Коэффициент корреляции и корреляционное отношение дают более точную информацию о характере и силе связи, чем картина корреляционного поля. Выборочный коэффициента корреляции определяют по формуле:
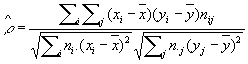 , ,
где
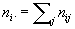 , , 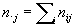 , ,
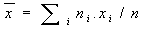 , , 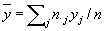 . .
При большом числе независимых наблюдений, подчиняющихся одному и тому же распределению, и при надлежащем выборе интервалов группировки коэффициент 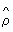 близок к истинному коэффициенту корреляции r. Поэтому использование близок к истинному коэффициенту корреляции r. Поэтому использование 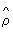 как меры связи имеет четко определенный смысл для тех распределений, для которых естественной мерой зависимости служит r (т. е. для нормальных или близких к ним распределений). Во всех др. случаях в качестве характеристики силы связи рекомендуется использовать корреляционное отношение h, интерпретация которого не зависит от вида исследуемой зависимости. как меры связи имеет четко определенный смысл для тех распределений, для которых естественной мерой зависимости служит r (т. е. для нормальных или близких к ним распределений). Во всех др. случаях в качестве характеристики силы связи рекомендуется использовать корреляционное отношение h, интерпретация которого не зависит от вида исследуемой зависимости.
Выборочное значение 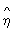 y|x вычисляется по данным корреляционной таблицы: y|x вычисляется по данным корреляционной таблицы:
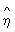 2y|x = 2y|x = 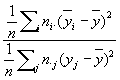
где числитель характеризует рассеяние условных средних значений 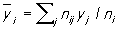 около безусловного среднего около безусловного среднего 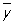 (аналогично определяется выборочное значение (аналогично определяется выборочное значение 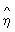 x|y). Величина x|y). Величина 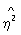 y|x y|x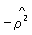 используется в качестве меры отклонения зависимости от линейной, т. к. обычно используется в качестве меры отклонения зависимости от линейной, т. к. обычно 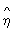 2y|x>r2, 2y|x>r2, 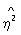 x|y>r2 и лишь в случае линейной зависимости r2= x|y>r2 и лишь в случае линейной зависимости r2=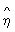 2y|x= 2y|x=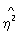 x|y. Так, при анализе корреляции между высотой и диаметром северной сосны было обнаружено, что условные средние значения высоты сосны для заданного диаметра связаны нелинейной зависимостью. Корреляционное отношение (высоты к диаметру) в этом случае равно 0,813, а коэффициент корреляции равен 0,762. x|y. Так, при анализе корреляции между высотой и диаметром северной сосны было обнаружено, что условные средние значения высоты сосны для заданного диаметра связаны нелинейной зависимостью. Корреляционное отношение (высоты к диаметру) в этом случае равно 0,813, а коэффициент корреляции равен 0,762.
Проверка гипотезы значимости связи основывается на знании законов распределения выборочных корреляционных характеристик. В случае нормального распределения величина выборочного коэффициента корреляции 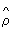 считается значимо отличной от нуля, если выполняется неравенство считается значимо отличной от нуля, если выполняется неравенство
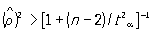 , ,
где ta есть критическое значение t-распределения Стьюдента с (n-2) степенями свободы, соответствующее выбранному уровню значимости a (см. Стьюдента распределение). Если же известно, что r ¹ 0, то необходимо воспользоваться z-преобразованием Фишера (не зависящим от r и n):
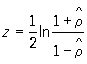 . .
Исходя из приближенной нормальности z, можно определить доверительные интервалы для истинного коэффициента корреляции r.
В случае когда изучаются не количественные признаки, а качественные, обычные меры зависимости не годятся. Однако, если удается каким-либо образом упорядочить изучаемые объекты в отношении некоторого признака, т. е. прописать им порядковые номера - ранги (по два номера в соответствии с двумя признаками), то в качестве выборочной характеристики связи можно воспользоваться, например, т. н. коэффициентом ранговой корреляции:
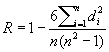 , ,
где di - разность рангов по обоим признакам для каждого объекта. По степени уклонения R от нуля можно сделать некоторое заключение о степени зависимости качественных признаков. Проверка гипотезы независимости признаков при небольшом объеме выборки производится с помощью специальных таблиц, а при n > 10 для вычисления критических значений выборочных коэффициентов пользуются тем, что эти величины распределены приближенно нормально.
Лит. см. при ст. Корреляция.
А. В. Прохоров. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|