|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Сферическая аберрация | Сферическая аберрация (далее С) один из типов аберраций оптических систем; проявляется в несовпадении фокусов для лучей света, проходящих через осе-симметрическую оптическую систему (линзу, объектив) на разных расстояниях от оптической оси этой системы (рис.). Фокус параксиального пучка лучей, который проходит через центральную зону системы h0h1, располагается в гауссовой плоскости Oh; фокусы пучков лучей, проходящих через другие кольцевые зоны (h1h2, h2h3 и т. д.), находятся ближе гауссовой плоскости для собирающих (положительных) систем и дальше для рассеивающих (отрицательных) систем. Вследствие С изображение, даваемое параллельным пучком лучей, будет на экране, перпендикулярном оси в точке О, иметь вид не точки, а кружка с ярким ядром и ослабевающим по яркости ореолом. При перемещении экрана вдоль оптической оси размеры этого кружка рассеяния и распределение в нем освещенности меняются. Для некоторого положения экрана кружок рассеяния имеет минимальные размеры (примерно в 4 раза меньше, чем в гауссовой плоскости). Различают продольную и поперечную С Первая измеряется длиной отрезка Оds` отсчитанной от гауссовой плоскости до фокуса лучей, прошедших через крайнюю зону оптической системы (h4h5 на рис.); поперечная С — радиусом кружка рассеяния Odz" в гауссовой плоскости, определяемым лучами, идущими от крайней зоны h4h5 Так как для собирающих линз Ods" < 0, а для рассеивающих Ods" > 0, то специальным подбором линз в оптической системе можно почти полностью устранить С У одиночных линз со сферическими поверхностями С можно уменьшить, выбирая оптимальное соотношение радиусов кривизны этих поверхностей. При преломления показателе материала линзы n = 1,5 С минимальна, если отношение радиусов равно 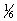 . Уменьшить С можно, используя оптические элементы с асферическими поверхностями (например, параболическими).
Лит.: Тудоровскиq А. Н., Теория оптических приборов, ч. 1, М.— Л., 1948; Русинов М. М., Техническая оптика, М.—Л., 1961; Волосов Д. С., Фотографическая оптика, М., 1971.
Л. Н. Капорский.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 22.12.2024 22:35:34
|
|
|
|
|
|
|
|
|
|
|
