
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Шаровые функции | Шаровые функции (далее Ш) однородные функции un степени п от прямоугольных координат х, у, z, удовлетворяющие уравнению Лапласа:
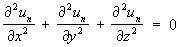
Существуют 2n + 1 линейно-независимых однородных многочленов от х, у, z целой положительной степени n, являющихся Ш: их линейная комбинация представляет общий вид такого многочлена степени n. Так, например,
uo= a, u1 = ax + by + cz;
u2 = a (x2 - z2) + b (y2 - z2) + cxy + dyz + ezx,
где a, b, с, d, e - произвольные постоянные, представляют общий вид однородных многочленов степеней 0, 1, 2, являющихся Ш Если вместо прямоугольных координат х, у, z ввести сферические координаты r, q, j, то Ш выражаются через сферические функции п (q,j) по формуле
un = rn n (q,j).
Каждой Ш un степени n соответствует Ш r ¾2n¾1 степени - n-1.
Ш применяются при нахождении общего решения уравнения Лапласа и при решении задач математической физики для областей, ограниченных сферическими поверхностями.
Лит. см. при статье Сферические функции.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 31.01.2026 12:06:33
|

|

|
 |
|

|
 |
 |
 |
|