
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Изменение функции | Изменение функции (далее И) вариация функции, одна из важнейших характеристик функции действительного переменного. Пусть функция f (x) задана на некотором отрезке (a, b); ее изменением, или полным изменением, на этом отрезке называется верхняя грань сумм
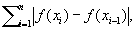
распространенная на всевозможные разбиения
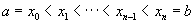
отрезка (a, b) на конечное число частей. Геометрически изменение непрерывной функции f (x) представляет собой длину проекции кривой у = f (x) на ось ординат, считая кратность покрытия (теорема Банаха). И f (x) на отрезке (а, b) принято обозначать символом
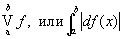 . .
Если функция f (x) имеет непрерывную производную, то
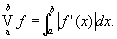
Свойства И: 1) если а < Ь < с, то
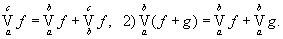
Существуют непрерывные функции, изменение которых бесконечно; например,
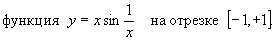
Если И конечно, то такая функция называется функцией с ограниченным изменением (функцией с конечным изменением, или функцией ограниченной вариации). Функции с ограниченным изменением были определены и впервые изучались К. Жорданом (1881). Многие важные функции принадлежат к числу функций с ограниченным изменением, например монотонные функции, заданные на отрезке, функции с конечным числом максимумов и минимумов, функции, удовлетворяющие Липшица условию. Всякая функция с ограниченным изменением на отрезке (а, b) имеет не более чем счетное множество разрыва точек, и притом первого рода, интегрируема по Риману и есть разность двух неубывающих функций (К. Жордан). Предел сходящейся последовательности функций с равностепенно ограниченными изменениями есть функция с ограниченным изменением. Функции с ограниченным изменением имеют почти всюду конечную производную, которая интегрируема по Лебегу (теорема А. Лебега).
Функции с ограниченным изменением имеют приложения в теории интеграла Стилтьеса, в теории тригонометрических рядов, в геометрии.
Лит.: Александров П. С. и Колмогоров А. Н., Введение в теорию функций действительного переменного, 3 изд., М. - Л., 1938; Kaмкe Э., Интеграл Лебега-Стилтьеса, пер. с нем., М., 1959; Лузин Н. Н., Интеграл и тригонометрический ряд, М. - Л., 1951; Лебег А., Интегрирование и отыскание примитивных функций, пер. с франц., М. - Л., 1934; Рудин У., Основы математического анализа, пер. с англ., М., 1966.
С. Б. Стечкин. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 31.01.2026 08:50:41
|

|

|
 |
|

|
 |
 |
 |
|