
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Функциональный анализ (математ.) | Функциональный анализ (далее Ф)часть современной математики, главной задачей которой является изучение бесконечномерных пространств и их отображений. Наиболее изучены линейные пространства и линейные отображения. Для Ф(математ.) характерно сочетание методов классического анализа, топологии и алгебры. Абстрагируясь от конкретных ситуаций, удается выделить аксиомы и на их основе построить теории, включающие в себя классические задачи как частный случай и дающие возможность решать новые задачи. Сам процесс абстрагирования имеет самостоятельное значение, проясняя ситуацию, отбрасывая лишнее и открывая неожиданные связи. В результате удается глубже проникнуть в сущность математических понятий и проложить новые пути исследования.
Развитие Ф(математ.) происходило параллельно с развитием современной теоретической физики, при этом выяснилось, что язык Ф(математ.) наиболее адекватно отражает закономерности квантовой механики, квантовой теории поля и т.п. В свою очередь эти физические теории оказали существенное влияние на проблематику и методы Ф(математ.)
1. Возникновение функционального анализа. Ф(математ.) как самостоятельный раздел математики сложился на рубеже 19 и 20 вв. Большую роль в формировании общих понятий Ф(математ.) сыграла созданная Г. Кантором теория множеств. Развитие этой теории, а также аксиоматической геометрии привело к возникновению в работах М. Фреше и Ф. Хаусдорфа метрической и более общей т. н. теоретико-множественной топологии, изучающей абстрактные пространства, т. е. множества произвольных элементов, для которых установлено тем или иным способом понятие близости.
Среди абстрактных пространств для математического анализа и Ф(математ.) оказались важными функциональные пространства (т. е. пространства, элементами которых являются функции - откуда и название "Ф(математ.)"). В работах Д. Гильберта по углублению теории интегральных уравнений возникли пространства l2 и L2(a, b) (см. ниже). Обобщая эти пространства, Ф. Рис изучил пространства lp и Lp (a, b), а С. Банах в 1922 выделил полные линейные нормированные пространства (банаховы пространства). В 1930-40-х гг. в работах Т. Карлемана, Ф. Риса, американских математиков М. Стоуна и Дж. Неймана была построена абстрактная теория самосопряженных операторов в гильбертовом пространстве.
В СССР первые исследования по Ф(математ.) появились в 30-х гг.: работы
А. Н. Колмогорова (1934) по теории линейных топологических пространств;
Н. Н. Боголюбова (1936) по инвариантным мерам в динамических системах;
Л. В. Канторовича (1937) и его учеников по теории полуупорядоченных пространств, применениям Ф(математ.) к вычислительной математике и др.; М. Г. Крейна и его учеников (1938) по углубленному изучению геометрии банаховых пространств, выпуклых множеств и конусов в них, теории операторов и связей с различными проблемами классического математического анализа и др.; И. М. Гельфанда и его учеников (1940) по теории нормированных колец (банаховых алгебр) и др.
Для современного этапа развития Ф(математ.) характерно усиление связей с теоретической физикой, а также с различными разделами классического анализа и алгебры, например теорией функций многих комплексных переменных, теорией дифференциальных уравнений с частными производными и т.п.
2. Понятие пространства. Наиболее общими пространствами, фигурирующими в Ф(математ.), являются линейные (векторные) топологические пространства, т. е. линейные пространства Х над полем комплексных чисел 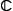 (или действительных чисел (или действительных чисел 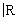 ), которые одновременно и топологические, причем линейные операции непрерывны в рассматриваемой топологии. Более частная, но очень важная ситуация возникает, когда в линейном пространстве Х можно ввести норму (длину) векторов, свойства которой являются обобщением свойств длины векторов в обычном евклидовом пространстве. Именно, нормой элемента x Î Х называется действительное число ||x|| такое, что всегда ||x|| ³ 0 и ||x|| = 0 тогда и только тогда, когда x = 0; ), которые одновременно и топологические, причем линейные операции непрерывны в рассматриваемой топологии. Более частная, но очень важная ситуация возникает, когда в линейном пространстве Х можно ввести норму (длину) векторов, свойства которой являются обобщением свойств длины векторов в обычном евклидовом пространстве. Именно, нормой элемента x Î Х называется действительное число ||x|| такое, что всегда ||x|| ³ 0 и ||x|| = 0 тогда и только тогда, когда x = 0;
||lx || = |l| ||x||, l Î 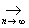 x, если ||xn - x|| x, если ||xn - x|| 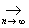 0. 0.
В большом числе задач возникает еще более частная ситуация, когда в линейном пространстве Х можно ввести скалярное произведение - обобщение обычного скалярного произведения в евклидовом пространстве. Именно, скалярным произведением элементов x, у Î Х называется комплексное число (x, у) такое, что всегда (x, x) ³ 0 и (x, x) = 0 тогда и только тогда, когда x = 0;
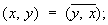 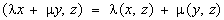 , l, m Î , l, m Î 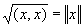 является нормой элемента x. Такое пространство называется предгильбертовым. Для конструкций Ф(математ.) важно, чтобы рассматриваемые пространства были полными (т. е. из того, что является нормой элемента x. Такое пространство называется предгильбертовым. Для конструкций Ф(математ.) важно, чтобы рассматриваемые пространства были полными (т. е. из того, что 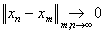 для xm, xn Î X, следует существование предела для xm, xn Î X, следует существование предела 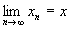 , также являющегося элементом Х). Полное линейное нормированное и полное предгильбертово пространства называются, соответственно, банаховым и гильбертовым. При этом известная процедура пополнения метрического пространства (аналогичная переходу от рациональных чисел к действительным) в случае линейного нормированного (предгильбертова) пространства приводит к банахову (гильбертову) пространству. , также являющегося элементом Х). Полное линейное нормированное и полное предгильбертово пространства называются, соответственно, банаховым и гильбертовым. При этом известная процедура пополнения метрического пространства (аналогичная переходу от рациональных чисел к действительным) в случае линейного нормированного (предгильбертова) пространства приводит к банахову (гильбертову) пространству.
Обычное евклидово пространство является одним из простейших примеров (действительного) гильбертова пространства. Однако в Ф(математ.) играют основную роль бесконечномерные пространства, т. е. такие, в которых существует бесконечное число линейно независимых векторов. Вот примеры таких пространств, элементами которых являются классы комплекснозначных (т. е. со значениями в 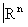 , норма ||x|| = , норма ||x|| = 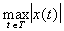 ; банахово пространство Lp (T) всех суммируемых с р-й (p ³ 1) степенью функций на Т, норма ; банахово пространство Lp (T) всех суммируемых с р-й (p ³ 1) степенью функций на Т, норма 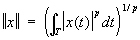 ; банахово пространство lp всех последовательностей таких, что ; банахово пространство lp всех последовательностей таких, что 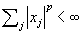 , здесь , здесь 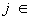  (множеству целых чисел), норма ||x|| =(å (множеству целых чисел), норма ||x|| =(å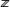 |xj|p)1/p; в случае p = 2 пространства l2 и L2 (T) гильбертовы, при этом, например, в L2(T) скалярное произведение |xj|p)1/p; в случае p = 2 пространства l2 и L2 (T) гильбертовы, при этом, например, в L2(T) скалярное произведение 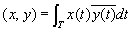 ; линейное топологическое пространство D ( ; линейное топологическое пространство D (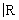 ), состоящее из бесконечно дифференцируемых функций на ), состоящее из бесконечно дифференцируемых функций на 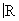 , каждая из которых финитна (т. е. равна нулю вне некоторого интервала (а, b)); при этом xn , каждая из которых финитна (т. е. равна нулю вне некоторого интервала (а, b)); при этом xn 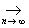 x, если xn (t) равномерно финитны (т. е. (а, b) не зависит от n) и сходятся равномерно со всеми своими производными к соответствующим производным x (t). x, если xn (t) равномерно финитны (т. е. (а, b) не зависит от n) и сходятся равномерно со всеми своими производными к соответствующим производным x (t).
Все эти пространства бесконечномерны, проще всего это видно для l2: векторы ej = {0,..., 0, 1, 0,...} линейно независимы.
С геометрической точки зрения наиболее простыми являются гильбертовы пространства Н, свойства которых больше всего напоминают свойства конечномерных евклидовых пространств. В частности, два вектора x, у Î Н называются ортогональными (x ^ y), если (x, у) = 0. Для любого x Î Н существует его проекция на произвольное подпространство - линейное замкнутое подмножество Н, т. е. такой вектор x, что x-x^f для любого f Î . Благодаря этому факту большое количество геометрических конструкций, имеющих место в евклидовом пространстве, переносится на Н, где они часто приобретают аналитический характер. Так, например, обычная процедура ортогонализации приводит к существованию в Н ортонормированного базиса - последовательности векторов ej, j Î 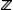 , из Н таких, что ||ej|| = 1, ej ^ ek при j ¹ k, и для любого x Î справедливо "покоординатное" разложение , из Н таких, что ||ej|| = 1, ej ^ ek при j ¹ k, и для любого x Î справедливо "покоординатное" разложение
x = å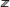 xjej (1) xjej (1)
где xj = (x, ej), ||x|| = å |xj|2 (для простоты Н предполагается сепарабельным, т. е. в нем существует счетное всюду плотное множество). Если в качестве Н взять L2(0, 2p) и положить |xj|2 (для простоты Н предполагается сепарабельным, т. е. в нем существует счетное всюду плотное множество). Если в качестве Н взять L2(0, 2p) и положить 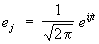 , j =...,-1, 0, 1..., то (1) даст разложение функции x (t) Î L2(0, 2p) в ряд Фурье, сходящийся в среднем квадратичном. Кроме того, соотношение (1) показывает, что соответствие между Н и l2 " {xj}, j Î , j =...,-1, 0, 1..., то (1) даст разложение функции x (t) Î L2(0, 2p) в ряд Фурье, сходящийся в среднем квадратичном. Кроме того, соотношение (1) показывает, что соответствие между Н и l2 " {xj}, j Î 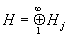 гильбертовых пространств j - конструкция, подобная образованию Н одномерными подпространствами, описываемому формулой (1); факторизация и пополнение: на исходном линейном пространстве Х задается квазискалярное произведение (т. е. возможно равенство (x, x) = 0 для x ¹ 0), часто весьма экзотического характера, и Н строится процедурой пополнения Х относительно (.,.) после предварительного отождествления с 0 векторов x, для которых (x, x) = 0; тензорное произведение гильбертовых пространств j - конструкция, подобная образованию Н одномерными подпространствами, описываемому формулой (1); факторизация и пополнение: на исходном линейном пространстве Х задается квазискалярное произведение (т. е. возможно равенство (x, x) = 0 для x ¹ 0), часто весьма экзотического характера, и Н строится процедурой пополнения Х относительно (.,.) после предварительного отождествления с 0 векторов x, для которых (x, x) = 0; тензорное произведение 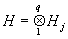 - образование его аналогично переходу от функций одной переменной f (x1) к функциям многих переменных f (x1,..., xq); проективный предел - образование его аналогично переходу от функций одной переменной f (x1) к функциям многих переменных f (x1,..., xq); проективный предел 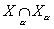 банаховых пространств - здесь банаховых пространств - здесь 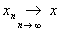 (грубо говоря), если (грубо говоря), если 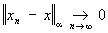 для каждого a; индуктивный предел для каждого a; индуктивный предел 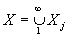 банаховых пространств X1 Ì X2 Ì..., здесь банаховых пространств X1 Ì X2 Ì..., здесь 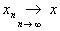 , если все xj, начиная с некоторого j0, лежат в одном Xj0, и в нем , если все xj, начиная с некоторого j0, лежат в одном Xj0, и в нем 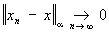 . Две последние процедуры обычно применяются для построения линейных топологических пространств. Таковы, например, ядерные пространства - проективный предел гильбертовых пространств Нa, обладающих тем свойством, что для каждого a найдется b такое, что hb Ì Нa, и это - т. н. вложение Гильберта - Шмидта (D ( . Две последние процедуры обычно применяются для построения линейных топологических пространств. Таковы, например, ядерные пространства - проективный предел гильбертовых пространств Нa, обладающих тем свойством, что для каждого a найдется b такое, что hb Ì Нa, и это - т. н. вложение Гильберта - Шмидта (D (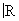 ) - пример ядерного пространства). ) - пример ядерного пространства).
Разработан важный раздел Ф, а., в котором изучаются пространства с конической структурой "x 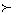 0" (полуупорядоченностью). Пример такого пространства - действительное С (Т), в нем считается x 0" (полуупорядоченностью). Пример такого пространства - действительное С (Т), в нем считается x  0, если x (t ³)0 для всех t ÎT. 0, если x (t ³)0 для всех t ÎT.
3. Операторы (общие понятия). Функционалы. Пусть X, - линейные пространства; отображение A: X ® называется линейным, если для x, у Î X, l, m Î 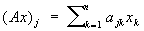 , ,
где x1,..., xn и (Ax)1,..., (Ax) n - координаты векторов x и Ax соответственно. При переходе к бесконечномерным линейным топологическим пространствам положение значительно усложняется. Здесь прежде всего необходимо различать непрерывные и разрывные линейные операторы (для конечномерных пространств они всегда непрерывны). Так, действующий из пространства L2 (а, b) в него же оператор
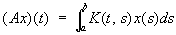 (2) (2)
(где (t, s) - ограниченная функция - ядро А) - непрерывен, в то время как определенный на подпространстве 1(a, b) Ì L2(a, b) оператор дифференцирования
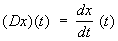 (3) (3)
является разрывным (вообще, характерной особенностью разрывных операторов является то, что они не определены на всем пространстве).
Непрерывный оператор A: X ® , где X, - банаховы пространства, характеризуется тем, что
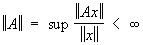 , ,
поэтому его называют также ограниченным. Совокупность всех ограниченных операторов 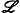 (X, ) относительно обычных алгебраических операций образует банахово пространство с нормой ||A||. Свойства (X, ) относительно обычных алгебраических операций образует банахово пространство с нормой ||A||. Свойства 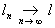 , если , если 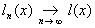 для каждого x Î X), относительно которой шар, т. е. множество точек x Î Х таких, что ||x|| £ r, уже будет компактным (такого эффекта никогда не будет в бесконечномерном пространстве относительно топологии, порождаемой нормой). Это позволяет более детально изучить ряд геометрических вопросов для множеств из X", например установить структуру произвольного компактного выпуклого множества как замкнутой оболочки своих крайних точек (теорема Крейна - Мильмана). для каждого x Î X), относительно которой шар, т. е. множество точек x Î Х таких, что ||x|| £ r, уже будет компактным (такого эффекта никогда не будет в бесконечномерном пространстве относительно топологии, порождаемой нормой). Это позволяет более детально изучить ряд геометрических вопросов для множеств из X", например установить структуру произвольного компактного выпуклого множества как замкнутой оболочки своих крайних точек (теорема Крейна - Мильмана).
Важной задачей Ф(математ.) является отыскание общего вида функционалов для конкретных пространств. В ряде случаев (помимо гильбертова пространства) это удается сделать, например (lp)¢, p > 1, состоит из функций вида å xjej, где xjej, где 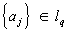 , , 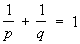 . Однако для большинства банаховых (и в особенности линейных топологических) пространств функционалы будут элементами новой природы, не конструирующимися просто средствами классического анализа. Так, например, при фиксированных t0 и m на пространстве D ( . Однако для большинства банаховых (и в особенности линейных топологических) пространств функционалы будут элементами новой природы, не конструирующимися просто средствами классического анализа. Так, например, при фиксированных t0 и m на пространстве D (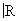 ) определен функционал ) определен функционал 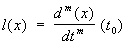 . В случае m = 0 его еще можно записать "классическим" образом - при помощи интеграла, однако при m ³ 1 это уже невозможно. Элементы из (D ( . В случае m = 0 его еще можно записать "классическим" образом - при помощи интеграла, однако при m ³ 1 это уже невозможно. Элементы из (D (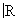 *(¢ называются обобщенными функциями (распределениями). Обобщенные функции как элементы сопряженного пространства можно строить и тогда, когда D ( *(¢ называются обобщенными функциями (распределениями). Обобщенные функции как элементы сопряженного пространства можно строить и тогда, когда D (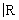 ) заменено другим пространством Ф, состоящим как из бесконечно, так и конечное число раз дифференцируемых функций; при этом существенную роль играют тройки пространств Ф" É Н É Ф, где Н - исходное гильбертово пространство, а Ф - линейное топологическое (в частности, гильбертово с др. скалярным произведением) пространство, например ) заменено другим пространством Ф, состоящим как из бесконечно, так и конечное число раз дифференцируемых функций; при этом существенную роль играют тройки пространств Ф" É Н É Ф, где Н - исходное гильбертово пространство, а Ф - линейное топологическое (в частности, гильбертово с др. скалярным произведением) пространство, например
Ф = l2(T).
Дифференциальный оператор D, фигурирующий в (3), будет непрерывным, если его понимать действующим в L2(a, b) из пространства 1(a, b), снабженного нормой 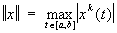 , , 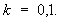 Однако для многих задач, и прежде всего для спектральной теории, такие дифференциальные операторы необходимо интерпретировать как действующие в одном и том же пространстве. Эти и другие близкие задачи привели к построению общей теории неограниченных, в частности неограниченных самосопряженных, и эрмитовых операторов. Однако для многих задач, и прежде всего для спектральной теории, такие дифференциальные операторы необходимо интерпретировать как действующие в одном и том же пространстве. Эти и другие близкие задачи привели к построению общей теории неограниченных, в частности неограниченных самосопряженных, и эрмитовых операторов.
4. Специальные классы операторов. Спектральная теория. Многие задачи приводят к необходимости изучать разрешимость уравнения вида Cx = y, где С - некоторый оператор, у Î - заданный, а x Î Х - искомый векторы. Например, если Х = = L2 (а, b), С = Е - А, где А - оператор из (2), а Е - тождественный оператор, то получается интегральное уравнение Фредгольма 2-го рода; если С - дифференциальный оператор, то получается дифференциальное уравнение, и т.п. Однако здесь нельзя рассчитывать на достаточно полную аналогию с линейной алгеброй, не ограничивая класс рассматриваемых операторов. Одним из важнейших классов операторов, наиболее близких к конечномерному случаю, являются компактные (вполне непрерывные) операторы, характеризующиеся тем, что переводят каждое ограниченное множество из Х в множество из , замыкание которого компактно (таков, например, оператор А из (2)). Для компактных операторов построена теория разрешимости уравнения x - Ax = у, вполне аналогичная конечномерному случаю (и содержащая, в частности, теорию упомянутых интегральных уравнений) (Ф. Рис).
В разнообразных задачах математической физики возникает т. н. задача на собственные значения: для некоторого оператора А: Х ® Х требуется выяснить возможность нахождения решения j ¹ 0 (собственного вектора) уравнения Аj = lj при некотором l Î 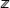 ljxjej, (4) ljxjej, (4)
где lj, - собственное значение, отвечающее ej. Для конечномерного Х вопрос о таком представлении полностью выяснен, при этом в случае кратных собственных значений для получения базиса в Х нужно, вообще говоря, добавить к собственным т. н. присоединенные векторы. Набор SpA собственных значений в этом случае называется спектром А.
Первое перенесение этой картины на бесконечномерный случай было дано для интегральных операторов типа А из (2) с симметричным ядром (т. е. (t, s) = (s, t) и действительно) (Д. Гильберт). Затем подобная теория была развита для общих компактных самосопряженных операторов в гильбертовом пространстве. Однако при переходе к простейшим некомпактным операторам возникли трудности, связанные с. самим определением спектра. Так, ограниченный оператор в L2(a, b)
(Tx)(t) = tx (t) (5)
не имеет собственных значений. Поэтому определение спектра было пересмотрено, обобщено и выглядит сейчас следующим образом.
Пусть Х - банахово пространство, А Î 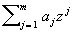 - многочлен, то f (A) = - многочлен, то f (A) = 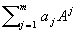 (степень оператора понимается как последовательное его применение). Однако если f (z) - аналитическая функция, то так прямо понимать f (A) уже не всегда возможно; в этом случае f (A) определяется следующей формулой, если f (z) аналитична в окрестности SpA, а Г - контур, охватывающий SpA и лежащий в области аналитичности f (z): (степень оператора понимается как последовательное его применение). Однако если f (z) - аналитическая функция, то так прямо понимать f (A) уже не всегда возможно; в этом случае f (A) определяется следующей формулой, если f (z) аналитична в окрестности SpA, а Г - контур, охватывающий SpA и лежащий в области аналитичности f (z):
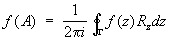 . (6) . (6)
При этом алгебраические операции над функциями переходят в аналогичные операции над операторами (т. е. отображение f (z) ® f (A) - гомоморфизм). Эти конструкции не дают возможности выяснить, например, вопросы полноты собственных и присоединенных векторов для общих операторов, однако для самосопряженных операторов, представляющих основной интерес, например, для квантовой механики, подобная теория полностью разработана.
Пусть Н - гильбертово пространство. Ограниченный оператор А: Н ® Н называется самосопряженным, если (Ax, у) = (x, Ау) (в случае неограниченного А определение более сложно). Если Н n-мерно, то в нем существует ортонормированный базис собственных векторов самосопряженного оператора А; другими словами, имеют место разложения:
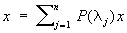 , , 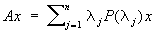 , (7) , (7)
где (lj) - оператор проектирования (проектор) на подпространство, натянутое на все собственные векторы оператора А, отвечающие одному и тому же собственному значению lj.
Оказывается, что эти формулы могут быть обобщены на произвольный самосопряженный оператор из Н, только сами проекторы (lj) могут не существовать, поскольку могут отсутствовать и собственные векторы (таков, например, оператор Т в (5)). В формулах (7) суммы заменяются теперь интегралами Стилтьеса по неубывающей операторнозначной функции Е (l) (которая в конечномерном случае равна 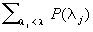 ), называется разложением единицы, или спектральной (проекторной) мерой, точки роста которой совпадают со спектром Sp А. Если привлечь обобщенные функции, то формулы типа (7) сохраняются. Именно, если имеется тройка Ф" É Н É Ф, где Ф, например, ядерно, причем А переводит Ф в Ф¢ и непрерывно, то соотношения (7) имеют место, только суммы переходят в интегралы по некоторой скалярной мере, а Е (l) теперь "проектирует" Ф в Ф¢, давая векторы из Ф¢, которые будут собственными в обобщенном смысле для А с собственным значением l. Аналогичные результаты справедливы для т. н. нормальных операторов (т. е. коммутирующих со своими сопряженными). Например, они верны для унитарных операторов - таких ограниченных операторов, которые отображают все Н на все Н и сохраняют при этом скалярное произведение. Для них спектр Sp расположен на окружности |z| = 1, вдоль которой и производится интегрирование в аналогах формул (6). См. также Спектральный анализ линейных операторов. ), называется разложением единицы, или спектральной (проекторной) мерой, точки роста которой совпадают со спектром Sp А. Если привлечь обобщенные функции, то формулы типа (7) сохраняются. Именно, если имеется тройка Ф" É Н É Ф, где Ф, например, ядерно, причем А переводит Ф в Ф¢ и непрерывно, то соотношения (7) имеют место, только суммы переходят в интегралы по некоторой скалярной мере, а Е (l) теперь "проектирует" Ф в Ф¢, давая векторы из Ф¢, которые будут собственными в обобщенном смысле для А с собственным значением l. Аналогичные результаты справедливы для т. н. нормальных операторов (т. е. коммутирующих со своими сопряженными). Например, они верны для унитарных операторов - таких ограниченных операторов, которые отображают все Н на все Н и сохраняют при этом скалярное произведение. Для них спектр Sp расположен на окружности |z| = 1, вдоль которой и производится интегрирование в аналогах формул (6). См. также Спектральный анализ линейных операторов.
5. Нелинейный функциональный анализ. Одновременно с развитием и углублением понятия пространства шло развитие и обобщение понятия функции. В конечном счете оказалось необходимым рассматривать отображения (не обязательно линейные) одного пространства в другое (часто - в исходное). Одной из центральных задач нелинейного Ф(математ.) является изучение таких отображений. Как и в линейном случае, отображение пространства в  ) называется функционалом. Для нелинейных отображений (в частности, нелинейных функционалов) можно различными способами определить дифференциал, производную по направлению и т.д. аналогично соответствующим понятиям классического анализа. Выделение из отображения квадратичного и т.д. членов приводит к формуле, аналогичной формуле Тейлора. ) называется функционалом. Для нелинейных отображений (в частности, нелинейных функционалов) можно различными способами определить дифференциал, производную по направлению и т.д. аналогично соответствующим понятиям классического анализа. Выделение из отображения квадратичного и т.д. членов приводит к формуле, аналогичной формуле Тейлора.
Важной задачей нелинейного Ф(математ.) является задача отыскания неподвижных точек отображения (точка x называется неподвижной для отображения , если Fx = x). К отысканию неподвижных точек сводятся многие задачи о разрешимости операторных уравнений, а также задачи отыскания собственных значений и собственных векторов нелинейных операторов. При решении уравнений с нелинейными операторами, содержащими параметр, возникает существенное для нелинейного Ф(математ.) явление - т. н. точки ветвления (решений).
При исследовании неподвижных точек и точек ветвления используются топологические методы: обобщения на бесконечномерные пространства теоремы Брауэра о существовании неподвижных точек отображений конечномерных пространств, степени отображений и т.п. Топологические методы Ф(математ.) развивались польским математиком Ю. Шаудером, французским математиком Ж. Лере, советскими математиками М. А. Красносельским, Л. А. Люстерником и др.
6. Банаховы алгебры. Теория представлений. На ранних этапах развития Ф(математ.) изучались задачи, для постановки и решения которых необходимы были лишь линейные операции над элементами пространства. Исключение составляют, пожалуй, только теория колец операторов (факторов) (Дж. Нейман, 1929) и теория абсолютно сходящихся рядов Фурье (Н. Винер, 1936). В конце 30-x гг. в работах японского математика М. Нагумо, советских математиков И. М, Гельфанда, Г. Е. Шилова, М. А. Наймарка и др. стала развиваться теория т. н. нормированных колец (современное название - банаховы алгебры), в которой, кроме операций линейного пространства, аксиоматизируется операция умножения (причем ||xy|| £ ||x|| ||y||). Типичными представителями банаховых алгебр являются кольца ограниченных операторов, действующих в банаховом пространстве Х (умножение в нем - последовательное применение операторов - необходимо с учетом порядка), различного рода функциональные пространства, например (T) с обычным умножением, L1(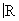 ) со сверткой в качестве произведения, и широкое обобщение их - класс т. н. групповых алгебр (топологические группы G), состоящих из комплекснозначных функций или мер, определенных на G со сверткой (в различных, не обязательно эквивалентных вариантах) в качестве умножения. ) со сверткой в качестве произведения, и широкое обобщение их - класс т. н. групповых алгебр (топологические группы G), состоящих из комплекснозначных функций или мер, определенных на G со сверткой (в различных, не обязательно эквивалентных вариантах) в качестве умножения.
Пусть 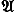 - коммутативная (т. е. xy = ух для любых x, у Î - коммутативная (т. е. xy = ух для любых x, у Î 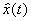 на М, причем сумме x + y и произведению xy соответствуют сумма и произведение функций. Другими словами, существует гомоморфизм на М, причем сумме x + y и произведению xy соответствуют сумма и произведение функций. Другими словами, существует гомоморфизм 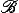 борелевских подмножеств G, инвариантная справа: для любых В Î борелевских подмножеств G, инвариантная справа: для любых В Î 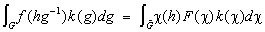 , где c(h) - характер группы G: непрерывная функция на G такая, что |c(h)| = 1 и c(h1h2) = c(h1)c(h2), dc - мера Хаара на группе характеров , где c(h) - характер группы G: непрерывная функция на G такая, что |c(h)| = 1 и c(h1h2) = c(h1)c(h2), dc - мера Хаара на группе характеров 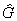 , а , а
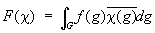 , ,
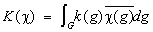
- обобщенное преобразование Фурье функций f (g) и k (g), которое продолжается до изоморфизма L2(G, dg) в L2(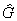 , dc). Для некоммутативных групп ситуация во многом усложняется. Если G компактна, то представление группы операторов сдвига (или, короче, группы сдвигов) удается хорошо описать; в этом случае L2(G, dg) распадается в прямую сумму конечномерных инвариантных относительно сдвигов подпространств. Если G некомпактна, то также получается разложение L2(G, dg) на более простые инвариантные части, но уже не в прямую сумму, а в прямой интеграл. , dc). Для некоммутативных групп ситуация во многом усложняется. Если G компактна, то представление группы операторов сдвига (или, короче, группы сдвигов) удается хорошо описать; в этом случае L2(G, dg) распадается в прямую сумму конечномерных инвариантных относительно сдвигов подпространств. Если G некомпактна, то также получается разложение L2(G, dg) на более простые инвариантные части, но уже не в прямую сумму, а в прямой интеграл.
Если G = 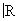 , то теория унитарных представлений может быть сведена к теории самосопряженных операторов. Именно, однопараметрическая группа унитарных операторов Тl, l Î , то теория унитарных представлений может быть сведена к теории самосопряженных операторов. Именно, однопараметрическая группа унитарных операторов Тl, l Î 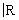 в гильбертовом пространстве Н допускает представление Тl = exp ilA, где А - самосопряженный оператор (теорема Стоун а); оператор А называется инфинитезимальным оператором (генератором) группы {Т"l}. Этот результат находит важные применения в изучении преобразований фазового пространства классической механики. Эта связь, а также приложения в статистической физике лежат в основе обширной ветви Ф(математ.) - эргодической теории. Связь между однопараметрическими группами преобразований и их генераторами допускает значительные обобщения: операторы Tl не обязаны быть унитарными, могут действовать в банаховых и более общих пространствах и даже быть определенными лишь для l ³ 0 (т. н. теория полугрупп операторов). Этот раздел Ф(математ.) имеет приложения в теории дифференциальных уравнений с частными производными и теории случайных (именно марковских) процессов. в гильбертовом пространстве Н допускает представление Тl = exp ilA, где А - самосопряженный оператор (теорема Стоун а); оператор А называется инфинитезимальным оператором (генератором) группы {Т"l}. Этот результат находит важные применения в изучении преобразований фазового пространства классической механики. Эта связь, а также приложения в статистической физике лежат в основе обширной ветви Ф(математ.) - эргодической теории. Связь между однопараметрическими группами преобразований и их генераторами допускает значительные обобщения: операторы Tl не обязаны быть унитарными, могут действовать в банаховых и более общих пространствах и даже быть определенными лишь для l ³ 0 (т. н. теория полугрупп операторов). Этот раздел Ф(математ.) имеет приложения в теории дифференциальных уравнений с частными производными и теории случайных (именно марковских) процессов.
Лит.: Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа 4 изд., М., 1976; Ахиезер Н. И., Глазман И. М., Теория линейных операторов в гильбертовом пространстве, 2 изд., М., 1966; Вулих Б. З., Введение в теорию полуупорядоченных пространств, М., 1961; Банах С. С., Курс функцioнального аналiзу Киïв, 1948; Рисс Ф., Секефальви-Надь Б., Лекции по функциональному анализу, пер. с франц., М., 1954; Соболев С. Л., Некоторые применения функционального анализа в математической физике, Л., 1950; Канторович Л. В., Акилов Г. П., Фв нормированных пространствах, М., 1959; Красносельский М. А., Забрейко П. П., Геометрические методы нелинейного анализа, М., 1975; Наймарк М. А., Нормированные кольца, 2 изд., М., 1968; Рудин У., Функциональный анализ, пер. с англ., М., 1975; Иосида К., Функциональный анализ, пер, с англ., М., 1967; Данфорд Н., Шварц Дж., Линейные операторы, пер. с англ., ч. 1-3, М., 1962-74; Хилле Э., Филлипс Р., Фи полугруппы, пер. с англ., 2 изд., М., 1962; Эдвардс Р. Э., Функциональный анализ. Теория и приложения пер с англ., М., 1969.
Ю. М. Березанский, Б. М. Левитан.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|