
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Ферма принцип | Ферма принцип (далее Ф) основной принцип геометрической оптики. Простейшая форма Ф – утверждение, что луч света всегда распространяется в пространстве между двумя точками по тому пути, по которому время его прохождения меньше, чем по любому из всех др. путей, соединяющих эти точки. Время прохождения светом расстояния l, заполненного средой с преломления показателем n, пропорционально оптической длине пути ; = 1•n для однородной среды, а при переменном n 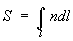 . Поэтому можно сказать, что Ф есть принцип наименьшей оптической длины пути. В первоначальной формулировке самого П. Ферма (около 1660) Ф имел смысл наиболее общего закона распространения света, из которого следовали все (к тому времени уже известные) законы геометрической оптики: для однородной среды он приводит к закону прямолинейности светового луча (в соответствии с геометрическим положением о том, что прямая есть кратчайшее расстояние между двумя точками), а для случая падения луча на границу различных сред из Ф можно получить законы отражения света и преломления света. В более строгой формулировке Ф представляет собой вариационный принцип, утверждающий, что реальный луч света распространяется от одной точки к другой по линии, по которой время его прохождения экстремально или одинаково по сравнению с временами прохождения по всем др. линиям, соединяющим эти точки. Это означает, что оптическая длина пути луча может быть не только минимальной, но и максимальной либо равной всем остальным возможным путям, соединяющим указанные точки. Примерами минимального пути служат упомянутые распространение света в однородной среде и прохождение светом границы двух сред с разными показателями преломления n. Все три случая (минимальности, максимальности и стационарности пути) можно проиллюстрировать, анализируя отражение луча света от вогнутого зеркала (рис.). . Поэтому можно сказать, что Ф есть принцип наименьшей оптической длины пути. В первоначальной формулировке самого П. Ферма (около 1660) Ф имел смысл наиболее общего закона распространения света, из которого следовали все (к тому времени уже известные) законы геометрической оптики: для однородной среды он приводит к закону прямолинейности светового луча (в соответствии с геометрическим положением о том, что прямая есть кратчайшее расстояние между двумя точками), а для случая падения луча на границу различных сред из Ф можно получить законы отражения света и преломления света. В более строгой формулировке Ф представляет собой вариационный принцип, утверждающий, что реальный луч света распространяется от одной точки к другой по линии, по которой время его прохождения экстремально или одинаково по сравнению с временами прохождения по всем др. линиям, соединяющим эти точки. Это означает, что оптическая длина пути луча может быть не только минимальной, но и максимальной либо равной всем остальным возможным путям, соединяющим указанные точки. Примерами минимального пути служат упомянутые распространение света в однородной среде и прохождение светом границы двух сред с разными показателями преломления n. Все три случая (минимальности, максимальности и стационарности пути) можно проиллюстрировать, анализируя отражение луча света от вогнутого зеркала (рис.).
К принципу Ферма: действительный путь света соответствует экстремальному времени распространения.
Если зеркало имеет форму эллипсоида вращения, а свет распространяется от одного его фокуса Р к другому Q (причем путь без отражения невозможен), то оптическая длина пути луча " + "Q по свойствам эллипсоида равна всем остальным возможным, например " + О" Q; если на пути между теми же точками свет отражается от зеркала меньшей, чем у эллипсоида, кривизны (MM), реализуется минимальный путь, если же большей (зеркало ) – максимальный. Условие экстремальности оптической длины пути сводится к требованию, чтобы была равна нулю вариация от интеграла 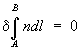 (см. Вариационное исчисление), где А и В – точки, между которыми распространяется свет. Это выражение и представляет собой математическую формулировку Ф (см. Вариационное исчисление), где А и В – точки, между которыми распространяется свет. Это выражение и представляет собой математическую формулировку Ф
В волновой теории света Ф представляет собой предельный случай Гюйгенса – Френеля принципа и применим, когда можно пренебречь дифракцией света (когда длина световой волны достаточно мала по сравнению с характерными для задачи размерами): рассматривая лучи как нормали к волновым поверхностям, легко показать, что при всяком распространении света оптической длины их путей будут иметь экстремальные значения. Во всех случаях, когда необходимо учитывать дифракцию, Ф перестает быть применимым.
Лит.: Fermat . de, CEuvres, t. 1–4, ., 1891–1912; Ландсберг Г. С., Оптика, 5 изд., М., 1976 (Общий курс физики); Крауфорд Ф., Волны, М., 1974 (Берклеевский курс физики, т. 3); Борн М., Вольф Э., Основы оптики, пер. с англ., 2 изд., М., 1973.
А. П. Гагарин.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|