
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Уравнение | Уравнение (далее У) в математике, аналитическая запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны. Аргументы, от которых зависят эти функции, называются обычно неизвестными, а значения неизвестных, при которых значения функций равны, – решениями (корнями); о таких значениях неизвестных говорят, что они удовлетворяют данному У Например, 3x – 6 = 0 является У с одним неизвестным, а х = 2 есть его решение; x2 + y2 = 25 является У с двумя неизвестными, а х = 3, y = 4 есть одно из его решений. Совокупность решений данного У зависит от области М значений, допускаемых для неизвестных. У может не иметь решений в М, тогда оно называется неразрешимым в области М. Если У разрешимо, то оно может иметь одно или несколько, или даже бесконечное множество решений. Например, У x4 – 4 = 0 неразрешимо в области рациональных чисел, но имеет два решения:
x1 = 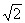 , x2 = – , x2 = –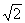 в области действительных чисел и четыре решения: x1 = в области действительных чисел и четыре решения: x1 = 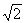 , x2 = – , x2 = – , x3 = i , x3 = i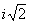 , x4 = – , x4 = – 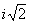 в области комплексных чисел. У sinx = 0 имеет бесконечное множество решений: xk = kp (k = 0, ± 1, ± 2,...) в области действительных чисел. Если У имеет решениями все числа области М, то оно называется тождеством в области М. Например, У х = в области комплексных чисел. У sinx = 0 имеет бесконечное множество решений: xk = kp (k = 0, ± 1, ± 2,...) в области действительных чисел. Если У имеет решениями все числа области М, то оно называется тождеством в области М. Например, У х = 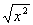 является тождеством в области неотрицательных чисел и не является тождеством в области действительных чисел. является тождеством в области неотрицательных чисел и не является тождеством в области действительных чисел.
Совокупность У, для которых требуется найти значения неизвестных, удовлетворяющие одновременно всем этим У, называется системой У; значения неизвестных, удовлетворяющих одновременно всем У системы, – решениями системы. Например, х + 2y = 5, 2x + у – z = 1 является системой двух У с тремя неизвестными; одним из решений этой системы является х = 1, у = 2, z = 3.
Две системы У (или два У) называются равносильными, если каждое решение одной системы (одного У) является решением др. системы (другого У), и наоборот, причем обе системы (оба У) рассматриваются в одной и той же области (см. Равносильные уравнения). Например, У х – 4 = 0 и 2x – 8 = 0 равносильны, т.к. решением обоих У является лишь х = 4. Всякая система У равносильна системе вида fk (x1, x2,..., хп) = 0, где k = 1, 2,... Процесс разыскания решений У заключается обычно в замене У равносильным. В некоторых случаях приходится заменять данное У другим, для которого совокупность решений шире, чем у данного У Решения нового У, не являющиеся решениями данного У, называются посторонними решениями (см. Посторонний корень).
Например, возводя в квадрат У  , получают У x - 3 = 4, решение которого х = 7 является посторонним для исходного У Поэтому, если при решении У делались действия, могущие привести к появлению посторонних решений (например, возведение У в квадрат), то все полученные решения преобразованного У проверяют подстановкой в исходное У , получают У x - 3 = 4, решение которого х = 7 является посторонним для исходного У Поэтому, если при решении У делались действия, могущие привести к появлению посторонних решений (например, возведение У в квадрат), то все полученные решения преобразованного У проверяют подстановкой в исходное У
Наиболее изучены У, для которых функции fk являются многочленами от переменных x1, x2,..., хп, – алгебраические У Например, алгебраическое У с одним неизвестным имеет вид:
a0xn + a1xn-1 +... + an = 0 (a0 ¹ 0); (*)
число n называется степенью У Решение алгебраич. У было одной из важнейших задач алгебры в 16–17 вв., когда были получены формулы и методы решения алгебраических У 3-й и 4-й степеней (см. Алгебра, Кардано формула) (правила решения алгебраических У 1-й и 2-й степеней были известны еще в глубокой древности). Для корней У 5-й и высших степеней общей формулы не существует, поскольку эти У, вообще говоря, не могут быть решены в радикалах (Н. Абель, 1824). Вопрос о разрешимости алгебраических У в радикалах привел (около 1830) Э. Галуа к общей теории алгебраических У (см. Галуа теория).
Каждое алгебраическое У всегда имеет хотя бы одно решение, действительное или комплексное. Это составляет содержание т. н. основной теоремы алгебры, строгое доказательство которой впервые было дано К. Гауссом в 1799. Если a – решение У (*), то многочлен a0xn + a1xn-1 +... + an делится на х – a. Если он делится на (х – a) k, но не делится на (х – a) k+1, то решение a имеет кратность k. Число всех решений У (*), если каждое считать столько раз, какова его кратность, равно n.
Если f (x) – трансцендентная функция, то У f (x) = 0 называются трансцендентным (см., например, Кеплера уравнение), причем в зависимости от вида f (x) оно называется тригонометрическим У, логарифмическим У, показательным У Рассматриваются также иррациональные У, то есть У, содержащие неизвестное под знаком радикала. При практическом решении У обычно применяются различные приближенные методы решения У
Среди систем У простейшими являются системы линейных У, то есть У, в которых fk суть многочлены первых степеней относительно x1, x2,..., хп (см. Линейное уравнение).
Решение системы У (не обязательно линейных) сводится, вообще говоря, к решению одного У при помощи т. н. исключения неизвестных (см. также Результант).
В аналитической геометрии одно У с двумя неизвестными интерпретируется при помощи кривой на плоскости, координаты всех точек которой удовлетворяют данному У Одно У с тремя неизвестными интерпретируется при помощи поверхности в трехмерном пространстве. При этой интерпретации решение системы У совпадает с задачей о разыскании точек пересечения линий, поверхностей и т.д. У с большим числом неизвестных интерпретируются при помощи многообразий в n-мерных пространствах.
В теории чисел рассматриваются неопределенные У, то есть У с несколькими неизвестными, для которых ищутся целые или же рациональные решения (см. Диофантовы уравнения). Например, целые решения У x2 + y2 = z2 вид х = m2-n2, у = 2 mn, z = m2 + n2 где m и n – целые числа.
С наиболее общей точки зрения, У является записью задачи о разыскании таких элементов некоторого множества А, что (a) = Ф (а), где и Ф – заданные отображения множества А в множество В. Если множества А и В являются множествами чисел, то возникают У рассмотренного выше вида. Если А и В – множества точек в многомерных пространствах, то получаются системы У, если же A и В – множества функций, то в зависимости от характера отображения могут получаться также дифференциальные уравнения, интегральные уравнения и др. виды У Наряду с вопросами нахождения решения У в общей теории У различного вида изучаются вопросы существования и единственности решения, непрерывной зависимости его от тех или иных данных и т.д.
Термин "У" употребляется (в отличном от указанного выше смысле) и в др. естественных науках, см., например, У времени (в астрономии), У состояния (в физике), Уравнения химические, Максвелла уравнения в электродинамике, Кинетическое уравнение Больцмана в теории газов.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|