
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Умножение | Умножение (далее У) операция образования по двум данным объектам а и b, называемым сомножителями, третьего объекта с, называемого произведением. У обозначается знаком Х (ввел англ. математик У Оутред в 1631) или • (ввел нем. ученый Г. Лейбниц в 1698); в буквенном обозначении эти знаки опускаются и вместо а ´ b или а • b пишут ab. У имеет различный конкретный смысл и соответственно различные конкретные определения в зависимости от конкретного вида сомножителей и произведения. У целых положительных чисел есть, по определению, действие, относящее числам а и b третье число с, равное сумме b слагаемых, каждое из которых равно а, так что ab = а + а +... + а (b слагаемых). Число а называется множимым, b – множителем. У дробных чисел  и и 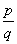 определяется равенством определяется равенством 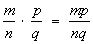 (см. Дробь). У рациональных чисел дает число, абсолютная величина которого равна произведению абсолютных величин сомножителей, имеющее знак плюс (+), если оба сомножителя одинакового знака, и знак минус (–), если они разного знака. У иррациональных чисел определяется при помощи У их рациональных приближений. У комплексных чисел, заданных в форме a = а + bi и b = с + di, определяется равенством ab = ac – bd + (ad + bc) i. При У комплексных чисел, записанных в тригонометрической форме: (см. Дробь). У рациональных чисел дает число, абсолютная величина которого равна произведению абсолютных величин сомножителей, имеющее знак плюс (+), если оба сомножителя одинакового знака, и знак минус (–), если они разного знака. У иррациональных чисел определяется при помощи У их рациональных приближений. У комплексных чисел, заданных в форме a = а + bi и b = с + di, определяется равенством ab = ac – bd + (ad + bc) i. При У комплексных чисел, записанных в тригонометрической форме:
a = r1 (cosj1 + isin j1),
b = r2 (cosj2 + isin j2),
их модули перемножаются, а аргументы складываются:
ab = r1r2{cos (j1 + j2) + i sin ((j1 + j2)}.
У чисел однозначно и обладает следующими свойствами:
1) ab = ba (коммутативность, переместительный закон);
2) a (bc) = (ab) c (ассоциативность, сочетательный закон);
3) a (b + c) = ab + ac (дистрибутивность, распределительный закон). При этом всегда а ×0 = 0; a×1 = а. Указанные свойства лежат в основе обычной техники У многозначных чисел.
Дальнейшее обобщение понятия У связано с возможностью рассматривать числа как операторы в совокупности векторов на плоскости. Например, комплексному числу r (cosj + i sin j) соответствует оператор растяжения всех векторов в r раз и поворота их на угол j вокруг начала координат. При этом У комплексных чисел отвечает У соответствующих операторов, т. е. результатом У будет оператор, получающийся последовательным применением двух данных операторов. Такое определение У операторов переносится и на другие виды операторов, которые уже нельзя выразить при помощи чисел (например, линейные преобразования). Это приводит к операциям У матриц, кватернионов, рассматриваемых как операторы поворота и растяжения в трехмерном пространстве, ядер интегральных операторов и т.д. При таких обобщениях могут оказаться невыполненными некоторые из перечисленных выше свойств У, чаще всего – свойство коммутативности (некоммутативная алгебра). Изучение общих свойств операции У входит в задачи общей алгебры, в частности теории групп и колец.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|