|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Собственные значения | Собственные значения (далее С) линейного преобразования или оператора А, числа l, для которых существует ненулевой вектор х такой, что Ах = lх; вектор х называется собственным вектором. Так, С дифференциального оператора L (y) с заданными краевыми условиями служат такие числа l, при которых уравнение L (y) = lу имеет ненулевое решение, удовлетворяющее этим краевым условиям. Например, если оператор L (y) имеет вид у", то его С при краевых условиях y (0) = у (p) = 0 служат числа вида ln = n2, где n — натуральное число, т.к. уравнению — у" = n2у с указанными краевыми условиями удовлетворяют функции уп = sin nx; если же ln ¹ n2 ни при каком натуральном n, то уравнению —у" = lу при тех же краевых условиях удовлетворяет только функция у (х) º 0. К изучению С линейных операторов приводят многие задачи математики, механики и физики (аналитической геометрии и алгебры, теории колебаний, квантовой механики и т.д.).
С матрицы 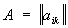 (i, k = 1, 2,..., n) называют С соответствующего ей линейного преобразования п-мерного комплексного пространства. Их можно определить также как корни определителя матрицы А — lЕ (где Е — единичная матрица), т. е. корни уравнения
 , (*)
называемого характеристическим уравнением матрицы. Эти числа совпадают для подобных матриц А и В–1 AB (где В — неособенная матрица) и характеризуют поэтому свойства линейного преобразования, не зависящие от выбора системы координат. Каждому корню li; уравнения (*) отвечает вектор xi ¹ 0 (собственный вектор) такой, что Axi = lixi. Если все С различны, то множество собственных векторов можно выбрать за базис векторного пространства. В этом базисе линейное преобразование описывается диагональной матрицей
 .
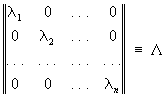Каждую матрицу А с различными С можно представить в виде С–1LС. Если А — самосопряженная матрица, то ее С действительны, собственные векторы ортогональны, а матрицу С можно выбрать унитарной (см. Унитарная матрица). Модуль каждого С унитарной матрицы равен 1. Сумма С матрицы равна сумме ее диагональных элементов, т. е. следу ее матрицы. Знание С матрицы играет важную роль в исследовании сходимости некоторых приближенных методов решения систем линейных уравнений. См. также Собственные функции.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
