
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Предельные теоремы | Предельные теоремы (далее П) теории вероятностей, общее название ряда теорем вероятностей теории, указывающих условия возникновения тех или иных закономерностей в результате действия большого числа случайных факторов. Исторически первые П — теорема Бернулли (1713) и теорема Лапласа (1812) — относятся к распределению отклонений частоты появления некоторого события Е при n независимых испытаниях от его вероятности р (0 < р < 1). Частотой называется отношение m/n, где m — число наступлений события Е при n испытаниях (точные формулировки см. в ст. Бернулли теорема и Лапласа теорема). С. Пуассон (1837) распространил эти теоремы на случай, когда вероятность pk наступления Е в k-м испытании может зависеть от k, описав предельное поведение при n ® ¥ распределения отклонений частоты m/n от среднего арифметического 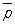 вероятностей pk (1 £ k £ n): вероятностей pk (1 £ k £ n):
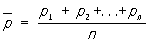
(см. Больших чисел закон). Если обозначить через Xk случайную величину, принимающую значение, равное единице при появлении события Е в k-м испытании, и значение, равное нулю при его непоявлении, то m можно представить в виде суммы
m = X1 + X2 +... + Xn,
что позволяет рассматривать перечисленные теоремы как частные случаи общих П, относящихся к суммам независимых случайных величин (закона больших чисел и центральной предельной теоремы).
Закон больших чисел. Пусть
X1, X2,..., Xn,... (*)
— какая-либо последовательность независимых случайных величин, sn — сумма первых n из них
sn = X1 + X2 +... + Xn,
An и 2n — соответственно математическое ожидание
An= Е sn = Е X1 + E X2 +... + EXn,
и дисперсия
2n= D sn -= D X1 +D X2 +... + DXn,
суммы sn. Говорят, что последовательность (*) подчиняется закону больших чисел, если при любом e > 0 вероятность неравенства
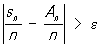
стремится к нулю при n ® ¥.
Широкие условия приложимости закона больших чисел найдены впервые П. Л. Чебышевым (в 1867) (см. Больших чисел закон). Эти условия затем были обобщены А. А. Марковым (старшим). Вопрос о необходимых и достаточных условиях приложимости закона больших чисел был окончательно решен А. Н. Колмогоровым (1928). В случае, когда величины Xn имеют одну и ту же функцию распределения, эти условия, как показал А. Я. Хинчин (1929), сводятся к одному: величины Xn должны иметь конечные математические ожидания.
Центральная предельная теорема. Говорят, что к последовательности (*) применима центральная предельная теорема, если при любых z1 и z2 вероятность неравенства
z1n < sn — An < z2n
имеет пределом при n ® ¥ — величину
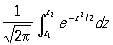
(см. Нормальное распределение). Довольно общие достаточные условия применимости центральной предельной теоремы были указаны Чебышевым (1887), но и в его доказательстве обнаружились пробелы, восполненные лишь позже Марковым (1898). Решение вопроса, близкое к окончательному, было получено А. М. Ляпуновым (1901). Точная формулировка теоремы Ляпунова такова: пусть
ck = E|Xk — ЕХк|2+d, d > 0
n = c1 + c2 +... + cn.
Если отношение 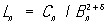 стремится к нулю при n ® ¥, то к последовательности (*) применима центральная предельная теорема. Окончательное решение вопроса об условиях приложимости центральной предельной теоремы получено в основных чертах С. Н. Бернштейном (1926) и дополнено В. Феллером (1935). стремится к нулю при n ® ¥, то к последовательности (*) применима центральная предельная теорема. Окончательное решение вопроса об условиях приложимости центральной предельной теоремы получено в основных чертах С. Н. Бернштейном (1926) и дополнено В. Феллером (1935).
Из др. направлений работ в области П можно отметить следующие.
1) Начатые Марковым и продолженные Бернштейном и др. исследования условий приложимости закона больших чисел и центральной предельной теоремы к суммам зависимых величин.
2) Даже в случае последовательности одинаково распределенных случайных величин можно указать простые примеры, когда суммы имеют в пределе распределение, отличное от нормального (речь идет о невырожденных распределениях, т. е. о распределениях, не сосредоточенных целиком в одной точке). В работах советских математиков А. Я. Хинчина, Б. В. Гнеденко, французских математиков П. Леви, В. Деблина и др. полностью изучены как класс возможных предельных распределении для сумм независимых случайных величин, так и условия сходимости распределений сумм к тому или иному предельному распределению.
3) Значительное внимание уделяется т. н. локальным П Пусть, например, величины Xn принимают лишь целые значения. Тогда суммы sn принимают также только целые значения и естественно поставить вопрос о предельном поведении вероятностей n (m) того, что sn = m (где m — целое). Простейшим примером локальной П может служить локальная теорема Лапласа (см. Лапласа теорема).
4) П в их классической постановке описывают поведение отдельной суммы sn с возрастанием номера n. Достаточно общие П для вероятностей событий, зависящих сразу от нескольких сумм, получены впервые Колмогоровым (1931). Так, например, из его результатов следует, что при весьма широких условиях вероятность неравенства
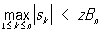
имеет пределом величину
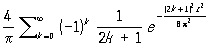 (z > 0) (z > 0)
5) Перечисленные выше П, т. относятся к суммам случайных величин. Примером П иного рода могут служить П для членов вариационного ряда. Эти П подробно изучены советскими математиками Б. В. Гнеденко и Н. В. Смирновым.
6) Наконец, к П относят также и теоремы, устанавливающие свойства последовательностей случайных величин, имеющие место с вероятностью, равной единице (см., например, Повторного логарифма закон).
Лит.: Гнеденко Б. В., Колмогоров А. Н., Предельные распределения для сумм независимых случайных величин, М. — Л., 1949; Ибрагимов И. А., Линник Ю. В., Независимые и стационарно связанные величины, М., 1965; Прохоров Ю. В., Розанов Ю. А., Теория вероятностей. Основные понятия. П. Случайные процессы, 2 изд., М., 1973.
Ю. В. Прохоров. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|