
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Нормальная (жорданова) форма матриц | Нормальная (жорданова) форма матриц (далее Н). С каждой квадратной матрицей 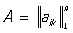 связан целый класс матриц, подобных матрице А. В этом классе всегда существует матрица, имеющая специальную нормальную (или каноническую) жорданову форму (термин "Нормальная (жорданова) форма матриц (ж.) ф. м." связан с именем К. Жордана). На схеме показана жорданова форма некоторой матрицы 8-го порядка: связан целый класс матриц, подобных матрице А. В этом классе всегда существует матрица, имеющая специальную нормальную (или каноническую) жорданову форму (термин "Нормальная (жорданова) форма матриц (ж.) ф. м." связан с именем К. Жордана). На схеме показана жорданова форма некоторой матрицы 8-го порядка:
 (1) (1)
Вдоль главной диагонали расположены специальные квадратные клетки (на схеме они обведены пунктиром). Все элементы матрицы, расположенные вне этих клеток, равны нулю. В каждой диагональной клетке вдоль главной диагонали повторяется одно и то же (комплексное) число (в первой клетке l1, во второй l2 и т.д.); параллельный ряд над главной диагональю состоит из единиц. Все же остальные элементы в диагональных клетках равны нулю. На приведенной схеме имеются три диагональные клетки, из которых первая имеет порядок 4, вторая и третья - порядок 2. В общем же случае число клеток и порядки их могут быть любыми. Среди чисел l1, l2,... возможны и равные. Исходная матрица А в указанном примере имеет следующие элементарные делители: (l - l1)4, (l - l2)2, (l - l3)2. По элементарным делителям матрицы однозначно определяется ее жорданова форма.
Если матрица А имеет жорданову форму , то существует неособенная матрица Т такая, что А = TIT-1. Замену матрицы А подобной ей матрицей называют приведением матрицы А к нормальной жордановой форме.
Представление о применениях жордановой формы матрицы можно получить на примере системы линейных дифференциальных уравнений с постоянными коэффициентами:
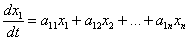
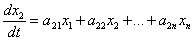
……………………………………….
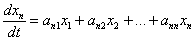
в матричной записи:
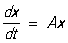
Введем новые неизвестные функции y1, у2,... yn при помощи неособенной матрицы 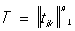 (tik - числа (i, k = 1, 2, …, n)): (tik - числа (i, k = 1, 2, …, n)):
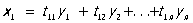 , ,
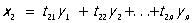 , ,
…………………………………….
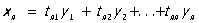 ; ;
в матричной записи:
х = Ту.
Подставляя это выражение для x в (2), получим:
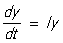
где матрица связана с матрицей А равенством:
А=TIT-1.
Обычно матрицу Т подбирают так, чтобы матрица А имела жорданову форму. В этом случае система уравнений (3) значительно проще системы (2). Так, например, при n = 8, если матрица 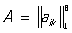 имеет жорданову форму (1), то система (3) будет иметь вид: имеет жорданову форму (1), то система (3) будет иметь вид:
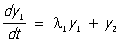 , ,  , ,
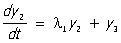 , ,  , ,
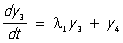 , , 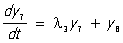 , ,
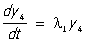 , , 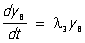 . .
Интегрирование такой системы сводится к многократному интегрированию одного дифференциального уравнения.
Лит. см. при ст. Матрица.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|