
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Неравенства (матем.) | Неравенства (далее Н) (математические), соотношения между числами или величинами, указывающие, какие из них больше других. Для обозначения Н (матем.) употребляется знак <, обращенный острием к меньшему числу. Так, соотношения 2 > 1 и 1 < 2 выражают одно и то же, а именно: 2 больше 1, или 1 меньше 2. Иногда несколько Н (матем.) записываются вместе (например, а < b < с). Желая выразить, что из двух чисел а и b первое или больше второго, или равно ему, пишут: а ³ b (или b £ а) и читают: "а больше или равно b" (или "b меньше или равно а") либо короче: "а не меньше b" (или "b не больше а"). Запись а ¹ b означает, что числа а и b не равны, но не указывает, какое из них больше. Все эти соотношения также называются Н (матем.)
Н (матем.) обладают многими свойствами, общими с равенствами. Так, Н (матем.) остается справедливым, если к обеим частям его прибавить (или от обеих частей отнять) одно и то же число. Точно так же можно умножать обе части Н (матем.) на одно и то же положительное число. Однако если обе части Н (матем.) умножить на отрицательное число, то смысл Н (матем.) изменится на обратный (т. е. знак > заменяется на <, а < на >). Из неравенства А < В и С < D следует А + С < В + D и А - D < В - С, т. е. одноименные Н (матем.) (А < В и С < D) можно почленно складывать, а разноименные Н (матем.) (А < В и D > С) — почленно вычитать. Если числа А, В, С и D положительны, то из неравенств А < В и С < D следует также AC < BD и A/D < В/С, т. е. одноименные Н (матем.) (между положительными числами) можно почленно перемножать, а разноименные — почленно делить.
Н (матем.), в которые входят величины, принимающие различные числовые значения, могут быть верны для одних значений этих величин и неверны для других. Так, неравенство x2 — 4x + 3 > 0 верно при х = 4 и неверно при х = 2. Для Н (матем.) этого типа возникает вопрос об их решении, т. е. об определении границ, в которых следует брать входящие в Н (матем.) величины для того, чтобы Н (матем.) были справедливы. Так, переписывая неравенство x2 — 4x + 3 > 0 в виде: (х — 1)(х — 3) > 0, замечают, что оно будет верно для всех х, удовлетворяющих одному из следующих неравенств: х < 1, х > 3, которые и являются решением данного Н (матем.)
Укажем несколько типов Н (матем.), выполняющихся тождественно в той или иной области изменения входящих в них переменных.
1) Неравенство для модулей. Для любых действительных или комплексных чисел a1, a2,..., an справедливо Н (матем.)
|a1 + a2 + … + an £ a1| + a2 +... + an|.
2) Неравенство для средних. Наиболее известны Н (матем.), связывающие гармонические, геометрические, арифметические и квадратические средние:
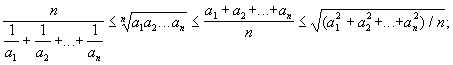
3) Линейные неравенства. Рассматривается система Н (матем.) Вида
ai1x1 + ai2x2 +... + ainxn (bi ³ i = 1, 2,..., m).
Совокупность решений этой системы Н (матем.) представляет собой некоторый выпуклый многогранник в n-мepном пространстве (x1, x2,..., xn); задача теории линейных Н (матем.) состоит в том, чтобы изучить свойства этого многогранника. Некоторые вопросы теории линейных Н (матем.) тесно связаны с теорией наилучших приближений, созданной П. Л. Чебышевым.
См. также Бесселя неравенство, Буняковского неравенство, Гельдера неравенство, Коши неравенство, Минковского неравенство.
Н (матем.) имеют существенное значение для всех разделов математики. В теории чисел целый раздел этой дисциплины — диофантовы приближения — полностью основан на Н (матем.); аналитическая теория чисел тоже часто оперирует с Н (матем.) В алгебре дается аксиоматическое обоснование Н (матем.); линейные Н (матем.) играют большую роль в теории линейного программирования. В геометрии Н (матем.) постоянно встречаются в теории выпуклых тел и в изопериметрических задачах. В теории вероятностей многие законы формулируются с помощью Н (матем.) (см., например, Чебышева неравенство). В теории дифференциальных уравнений используются так называемые дифференциальные Н (матем.) (см., например, Чаплыгина метод). В теории функций постоянно употребляются различные Н (матем.) для производных от многочленов и тригонометрических полиномов. В функциональном анализе при определении нормы в функциональном пространстве требуется, чтобы она удовлетворяла Н (матем.) треугольника
||х + у|| £ ||x|| + ||y||.
Многие классические Н (матем.) в сущности определяют значения нормы линейного функционала или линейного оператора в том или ином пространстве или дают оценки для них.
Лит.: Коровкин П. П., Н, 3 изд., М., 1966; Харди Г. Г., Литтльвуд Дж. Е., Полиа Г., Н, пер. с англ., М., 1948.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|