
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Непрерывная функция | Непрерывная функция (далее Н) функция, получающая бесконечно малые приращения при бесконечно малых приращениях аргумента. Однозначная функция f (x) называется непрерывной при значении аргумента x0, если для всех значений аргумента х, отличающихся достаточно мало от x0, значения функции f (x) отличаются сколь угодно мало от ее значения f (x0). Точнее, функция f (х) называется непрерывной при значении аргумента x0 (или, как говорят, в точке x0), если каково бы ни было e > 0, можно указать такое d > 0, что при |х — х0| < d будет выполняться неравенство |f (x) — f (x0)| < e. Это определение равносильно следующему: функция f (x) непрерывна в точке x0, если при х, стремящемся к x0, значение функции f (x) стремится к пределу f (x0). Если все условия, указанные в определении Н, выполняются только при х ³ х0 или только при х £ х0, то функция называется, соответственно, непрерывной справа или слева в точке x0. Функция f (x) называется непрерывной н а отрезке (а, b), если она непрерывна в каждой точке х при а < х < b и, кроме того, в точке а непрерывна справа, а в точке b — слева.
Понятию Н противопоставляется понятие разрывной функции. Одна и та же функция может быть непрерывной для одних и разрывной для других значений аргумента. Так, дробная часть числа х (ее принято обозначать через (х)), например
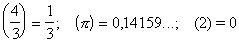
является функцией разрывной при любом целом значении и непрерывной при всех других значениях (рис. 1), причем в целочисленных точках она непрерывна справа.
Простейшими функциями переменного х, непрерывными при всяком значении x, являются многочлены, синус (у = sin x), косинус (у = cos x), показательная функция (у = ax, где а — положительное число). Сумма, разность и произведение Н снова дают Н Частное двух Н также есть Н, за исключением тех значений х, для которых знаменатель обращается в нуль (так как в таких точках рассматриваемое частное не определено). Например,
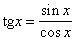
есть Н для всех значений х, кроме нечетных кратных p/2, при которых cosх обращается в нуль.
Н обладают многими важными свойствами, которыми и объясняется огромное значение этих функций в математике и ее приложениях. Одно из важнейших свойств выражается следующей теоремой: для всякой функции, непрерывной на отрезке (а, b) можно найти многочлен, значения которого отличаются на этом отрезке от значений функции менее чем на произвольно малое, наперед заданное число (теорема о приближении Н многочленами). Справедлива также и обратная теорема: всякая функция, которую на некотором отрезке можно с произвольной степенью точности заменить многочленом, непрерывна на этом отрезке.
Функция, непрерывная на отрезке, ограничена на нем и достигает на этом отрезке наибольшего и наименьшего значения (см. Наибольшее и наименьшее значения функций). Кроме того, она принимает на этом отрезке все значения, лежащие между ее наименьшим и наибольшим значениями. Функции, непрерывные на отрезке, обладают свойством равномерной непрерывности. Всякая функция, непрерывная на некотором отрезке, интегрируема на нем, т. е. является производной другой Н Однако не всякая Н сама имеет производную. Геометрически это означает, что график Н не обязательно обладает в каждой точке определенным направлением (касательной); это может произойти, например, потому, что график имеет угловую точку (рис.2, функция у = |x|), или потому, что он совершает в любой близости точки О бесконечно много колебаний между двумя пересекающимися прямыми (рис. 3, функция
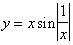
при х ¹ 0 и y = 0 при x = 0).
Существуют Н, не имеющие производной ни в одной точке (первый пример такого рода был найден Б. Больцано). Представление о графике подобной функции дает рис. 4, где изображены первые этапы построения, состоящего в неограниченно продолжающейся замене средней трети каждого прямолинейного отрезка двузвенными ломаными; соотношения длин подбираются так, чтобы в пределе получить Н
Функция (x, у, z,...) нескольких переменных, определенная в некоторой окрестности точки (x0, y0, z0,...), называется непрерывной в этой точке, если для любого e > 0 можно указать такое d > О, что при одновременном выполнении неравенств: |x — x0| < d, |у — у0| < d, |z — z0| < d,... выполняется также и неравенство:
(x, у, z,...) — (x0, y0, z0,...)| < e.
Такая функция будет непрерывной по отношению к каждому аргументу в отдельности (если остальным аргументам приданы определенные числовые значения). Обратное, однако, неверно: функция (x:, у, z,...), непрерывная по каждому аргументу в отдельности, может и не быть Н этих аргументов. Простейший пример этого дает функция (x, у), равная xy/(x2 + y2), если x2 + y2 ¹ 0, и равная 0 при x = у = 0. Она непрерывна по x при любом фиксированном значении y по y — при любом фиксированном значении х. В частности, она непрерывна по x при у = 0 и по y при x = 0. Если же положить, например, у = х ¹ 0, то значение функции будет оставаться равным x2/(x2 + y2) = 1/2, т. е. нельзя будет указать такого числа d > 0, чтобы при одновременном выполнении неравенств |х| < d, |у| < d выполнялось неравенство |ху/(х2 + y2)| < e. На Н нескольких переменных распространяются все основные теоремы, относящиеся к Н одного переменного.
Лит.: Хинчин А. Я., Краткий курс математического анализа, М., 1953; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|