
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Непрерывная дробь | Непрерывная дробь (далее Н) цепная дробь, один из важнейших способов представления чисел и функций. Н есть выражение вида
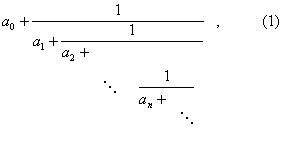
где a0 — любое целое число, a1, a2,..., an,... — натуральные числа, называемые неполными частными, или элементами, данной Н К Н, изображающей некоторое число a, можно прийти, записывая это число в виде
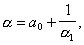
где a0 — целое число и 0 < 1/a1 < 1, затем, записывая в таком же виде a1 и т. д. Число элементов Н может быть конечным или бесконечным; в зависимости от этого Н называют конечной или бесконечной. Н (1) часто символически обозначают так:
(а0; a1, a2,..., an,...) (бесконечная Н) (2)
или
(а0; а1, a2,..., an) (конечная Н). (3)
Конечная Н всегда представляет собой рациональное число; обратно, каждое рациональное число может быть представлено в виде конечной Н (3); такое представление единственно, если потребовать, чтобы an ¹ 1. Н (а0; a1, a2,..., ak) (k £ n), записанную в виде несократимой дроби pk/qk, называют подходящей дробью порядка k данной Н (2). Числители и знаменатели подходящих дробей связаны рекуррентными формулами:
pk+1 = ak+1pk + pk-1, qk+1 = ak+1qk + qk-1,
которые служат основанием всей теории Н Из этих формул непосредственно вытекает важное соотношение
pkqk-1 — qkpk-1 = ± 1.
Для каждой бесконечной Н существует предел
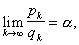
называемый значением данной Н Каждое иррациональное число является значением единственной бесконечной Н, получаемой разложением a указанным выше образом, например
(е — 1)/2 = (0, 1,6, 10,14, 18,...);
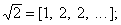
квадратичные иррациональности разлагаются в периодические Н
Основное значение Н для приложений заключается в том, что подходящие дроби являются наилучшими приближениями числа a, то есть, что для любой другой дроби m/n, знаменатель которой не более gk имеет место неравенство |na — m| > |gka — pkl; при этом |qk. — pk| < 1/qk+1. Нечетные подходящие дроби больше a, а четные — меньше. При возрастании k нечетные подходящие дроби убывают, а четные возрастают.
Н используются для приближения иррациональных чисел рациональными. Например, известные приближения 22/7, 355/113 для числа p (отношения длины окружности к диаметру) суть подходящие дроби для разложения p в Н Следует отметить, что первое доказательство иррациональности чисел е и p было дано в 1766 немецким математиком И. Ламбертом с помощью Н Французский математик Ж. Лиувилль доказал: для любого алгебраического числа a степени n можно найти такую постоянную l, что для любой дроби x/y выполняется неравенство |a — x/y| > l/уn. С помощью Н можно построить числа a такие, что разность |a — pk/qk| делается меньше a/gk, какую бы постоянную l мы ни взяли. Так, используя Н, можно строить трансцендентные числа. Недостатком Н является чрезвычайная трудность арифметических действий над ними, равносильная практической невозможности этих действий; например, зная элементы двух дробей, мы не можем сколько-нибудь просто получить элементы их суммы или произведения.
Н встречаются уже в 16 в. у Р. Бомбелли. В 17 в. Н изучал Дж. Валлис; ряд важных свойств Н открыл Х. Гюйгенс, занимавшийся ими в связи с теорией зубчатых колес. Многое сделал для теории Н Л. Эйлер в 18 в.
В 19 в. П. Л. Чебышев, А. А. Марков и др. применили Н, элементами которых являются многочлены, к изучению ортогональных многочленов.
Лит.: Чебышев П. Л., Полное собрание сочинений, 2 изд., т. 1, М. — Л., 1946; Хинчин А. Я., Цепные дроби, 2 изд., М. — Л., 1949; Эйлер Л., Введение в анализ бесконечно малых, пер. с лат., т. 1, М. — Л., 1936; Стилтьес Т. И., Исследования о непрерывных дробях, пер. с франц., Хар. — К., 1936; Perron О., Die Lehre von den Kettenbrüchen, 2 Aufl., Lpz. — ., 1929; Wall Н. ., Analytic theory of continued fractions, Toronto — . . — L., 1948.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|