
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Линейный оператор | Линейный оператор (далее Л), обобщение понятия линейного преобразования на линейные пространства. Линейным оператором на линейном пространстве Е называют функцию (x), определенную для всех х Î Е, значения которой суть элементы линейного пространства E1, и обладающую свойством линейности:
((x + (у) = ((x) + ((y),
где х и у — любые элементы из Е, a и b — числа. Если пространства Е и E1 нормированы и величина 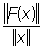 ограничена, то Л называют ограниченным, а ограничена, то Л называют ограниченным, а 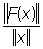 его нормой. его нормой.
Важнейшими конкретными примерами Л в функциональных пространствах являются дифференциальные Л
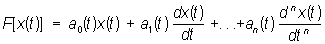
и интегральные Л
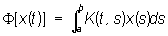
примером Л функций многих переменных может служить Лапласа оператор. Теория Л находит большое применение в различных вопросах математической физики и прикладной математики. См. также Функциональный анализ, Операторов теория, Спектральный анализ (математический), Собственные значения и собственные функции, Собственные векторы. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|