
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Квантовая теория поля | Квантовая теория поля. (далее К)
К— квантовая теория систем с бесконечным числом степеней свободы (полей физических). К/b>, возникшая как обобщение квантовой механики в связи с проблемой описания процессов порождения, поглощения и взаимных превращений элементарных частиц, нашла затем широкое применение в теории твердого тела, ядра атомного и др. и является теперь основным теоретическим методом исследования квантовых систем.
. Частицы и поля квантовой теории
1. Двойственность классической теории. В классической теории, формирование которой в основном завершилось к началу 20 в., физическая картина мира складывается из двух элементов — частиц и полей. Частицы — маленькие комочки материи, движущиеся по законам классической механики Ньютона. Каждая из них имеет 3 степени свободы: ее положение задается тремя координатами, например х, y, z, если зависимость координат от времени известна, то это дает исчерпывающую информацию о движении частицы. Описание полей значительно сложнее. Задать, например, электрическое поле — значит задать его напряженность Е во всех точках пространства. Т. о., для описания поля необходимо знать не 3 (как для материальной точки), а бесконечно большое число величин в каждый из моментов времени; иначе говоря, поле имеет бесконечное число степеней свободы. Естественно, что и законы динамики электромагнитного поля, установление которых обязано в основном исследованиям М. Фарадея и Дж. Максвелла, оказываются сложнее законов механики.
Указанное различие между полями и частицами является главным, хотя и не единственным: частицы дискретны, а поля непрерывны; электромагнитное поле (электромагнитные волны) может порождаться и поглощаться, в то время как материальным точкам классической механики возникновение и исчезновение чуждо; наконец, электромагнитные волны могут, накладываясь, усиливать или ослаблять и даже полностью "гасить" друг друга (интерференция волн), чего, разумеется, не происходит при наложении потоков частиц. Хотя частицы и волны переплетены между собой сложной сетью взаимодействий, каждый из этих объектов выступает как носитель принципиально различных индивидуальных черт. Картине мира в классической теории присущи отчетливые черты двойственности. Открытие квантовых явлений поставило на место этой картины другую, которую можно назвать двуединой.
2. Кванты электромагнитного поля. В 1900 М. Планк для объяснения закономерностей теплового излучения тел впервые ввел в физику понятие о порции, или кванте, излучения. Энергия E такого кванта пропорциональна частоте n излучаемой электромагнитной волны, E = hn, где коэффициент пропорциональности h = 6,62×10–27 эрг×сек (позднее он был назван постоянной Планка). А. Эйнштейн обобщил эту идею Планка о дискретности излучения, предположив, что такая дискретность не связана с каким-то особым механизмом взаимодействия излучения с веществом, а внутренне присуща самому электромагнитному излучению. Электромагнитное излучение "состоит" из таких квантов — фотонов. Эти представления получили экспериментальное подтверждение — на их основе были объяснены закономерности фотоэффекта и Комптона эффекта.
Т. о., электромагнитному излучению присущи черты дискретности, которые прежде приписывались лишь частицам. Подобно частице (корпускуле), фотон обладает определенной энергией, импульсом, спином и всегда существует как единое целое. Однако наряду с корпускулярными фотон обладает и волновыми свойствами, проявляющимися, например, в явлениях дифракции света и интерференции света. Поэтому его можно было бы назвать "волно-частицей".
3. Корпускулярно-волновой дуализм. Двуединое, корпускулярно-волновое представление о кванте электромагнитного поля — фотоне — было распространено Л. де Бройлем на все виды материи. И электроны, и протоны, и любые др. частицы, согласно гипотезе де Бройля, обладают не только корпускулярными, но и волновыми свойствами, Это количественно проявляется в соотношениях де Бройля, связывающих такие "корпускулярные" величины, как энергия E и импульс р частицы, с величинами, характерными для волнового описания, — длиной волны l и частотой n:
E = hn, p = n 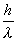 , (1) , (1)
где n — единичный вектор, указывающий направлениераспространения волны (см. Волны де Бройля). Корпускулярно-волновой дуализм (подтвержденный экспериментально) потребовал пересмотра законов движения и самих способов описания движущихся объектов. Возникла квантовая механика (или волновая механика). Важнейшей чертой этой теории является идея вероятностного описания движения микрообъектов. Величиной, описывающей состояние системы в квантовой механике (например, электрона, движущегося в заданном поле), является амплитуда вероятности, или волновая функция y(х, у, z, t). Квадрат модуля волновой функции, |y(х, у, z, t)|2, определяет вероятность обнаружить частицу в момент t в точке с координатами х, у, z. И энергия, и импульс, и все др. "корпускулярные" величины могут быть однозначно определены, если известна y(х, у, z, t). При таком вероятностном описании можно говорить и о "точечности" частиц, Это находит свое отражение в так называемой локальности взаимодействия, означающей, что взаимодействие, например, электрона с некоторым полем определяется лишь значениями этого поля и волновой функции электрона, взятыми в одной и той же точке пространства и в один и тот же момент времени. В классической электродинамике локальность означает, что точечный заряд испытывает воздействие поля в той точке, в которой он находится, и не реагирует на поле во всех остальных точках.
Являясь носителем информации о корпускулярных свойствах частицы, амплитуда вероятности y(х, у, z, t) в то же время отражает и ее волновые свойства. Уравнение, определяющее y(х, у, z, t), — Шредингера уравнение — является уравнением волнового типа (отсюда название — волновая механика); для y(х, у, z, t) имеет место суперпозиции принцип, что и позволяет описывать интерференционные явления.
Т. о., отмеченная выше двуединость находит отражение в самом способе квантовомеханического описания, устраняющего резкую границу, разделявшую в классической теории поля и частицы. Это описание продиктовано корпускулярно-волновой природой микрообъектов, и его правильность проверена на огромном числе явлений.
4. Ккак обобщение квантовой механики. Квантовая механика блестяще разрешила важнейшую из проблем — проблему атома, а также дала ключ к пониманию многих др. загадок микромира. Но в то же время самое "старое" из полей — электромагнитное поле — описывалось в этой теории классическими Максвелла уравнениями, т. е. рассматривалось по существу как классическое непрерывное поле. Квантовая механика позволяет описывать движение электронов, протонов и др. частиц, но не их порождение или уничтожение, т. е. применима лишь для описания систем с неизменным числом частиц. Наиболее интересная в электродинамике задача об испускании и поглощении электромагнитных волн заряженными частицами, что на квантовой языке соответствует порождению или уничтожению фотонов, по существу оказывается вне рамок ее компетенции. При квантовомеханическом рассмотрении, например, можно получить дискретный набор значений энергии электрона, момента количества движения и др. физических величин, относящихся к различным состояниям можно найти, какова вероятность обнаружить электрон на определенном расстоянии от ядра, но переходы из одного состояния в другое, сопровождающиеся испусканием или поглощением фотонов, описать нельзя (по крайней мере, последовательно). Т. о., квантовая механика дает лишь приближенное описание справедливое в той мере, в какой можно пренебречь эффектами излучения.
Порождаться и исчезать могут не только фотоны. Одно из самых поразительных и, как выяснилось, общих свойств микромира — универсальная взаимная превращаемость частиц. Либо "самопроизвольно" (на первый взгляд), либо в процессе столкновений одни частицы исчезают и на их месте появляются другие. Так, фотон может породить пару электрон-позитрон (см. Аннигиляция и рождение пар); при столкновении протонов и нейтронов могут рождаться пимезоны; пимезон распадается на мюон и нейтрино и т.д. Для описания такого рода процессов потребовалось дальнейшее развитие квантовой теории. Однако новый круг проблем не исчерпывается описанием взаимных превращений частиц, их порождения и уничтожения. Более общая и глубокая задача заключалась в том, чтобы "проквантовать" поле, т. е. построить квантовую теорию систем с бесконечным числом степеней свободы. Потребность в этом была тем более настоятельной, что, как уже отмечалось, установление корпускулярно-волнового дуализма обнаружило волновые свойства у всех "частиц". Решение указанных проблем и является целью того обобщения квантовой механики, которое называется К/b>
Чтобы пояснить переход от квантовой механики к К/b>, воспользуемся наглядной (хотя далеко не полной) аналогией. Рассмотрим сначала один гармонический осциллятор — материальную точку, колеблющуюся подобно маятнику. Переход от классической механики к квантовой при описании такого маятника выявляет ряд принципиально новых обстоятельств: допустимые значения энергии оказываются дискретными, исчезает возможность одновременного определения его координаты и импульса и т.д. Однако объектом рассмотрения по-прежнему остается один маятник (осциллятор), только величины, которые описывали его состояние в классической теории, заменяются, согласно общим положениям квантовой механики, соответствующими операторами.
Представим, что все пространство заполнено такого рода осцилляторами. Вместо того чтобы как-то "пронумеровать" эти осцилляторы, можно просто указывать координаты точек, в которых каждый из них находится, — так осуществляется переход к полю осцилляторов, число степеней свободы которого, очевидно, бесконечно велико.
Описание такого поля можно производить различными методами. Один из них заключается в том, чтобы проследить за каждым из осцилляторов. При этом на первый план выступают величины, называемые локальными, т. е. заданными для каждой из точек пространства (и момента времени), т.к. именно координаты "помечают" выбранный осциллятор. При переходе к квантовому описанию эти локальные классические величины, описывающие поле, заменяются локальными операторами. Уравнения, которые в классической теории описывали динамику поля, превращаются в уравнения для соответствующих операторов. Если осцилляторы не взаимодействуют друг с другом (или с некоторым др. полем), то для такого поля свободных осцилляторов общая картина, несмотря на бесконечное число степеней свободы, получается относительно простой; при наличии же взаимодействий возникают усложнения.
Другой метод описания поля основан на том, что вся совокупность колебаний осцилляторов может быть представлена как набор волн, распространяющихся в рассматриваемом поле. В случае невзаимодействующих осцилляторов волны также оказываются независимыми; каждая из них является носителем энергии, импульса, может обладать определенной поляризацией. При переходе от классического рассмотрения к квантовому, когда движение каждого осциллятора описывается вероятностными квантовыми законами, волны также приобретают вероятностный смысл. Но с каждой такой волной (согласно корпускулярно-волновому дуализму) можно сопоставить частицу, обладающую той же, что и волна, энергией и импульсом (а следовательно, и массой) и имеющую спин (классическим аналогом которого является момент количества движения циркулярно поляризованной волны). Эту "частицу", конечно, нельзя отождествить ни с одним из осцилляторов поля, взятым в отдельности, — она представляет собой результат процесса, захватывающего бесконечно большое число осцилляторов, и описывает некое возбуждение поля. Если осцилляторы не независимы (есть взаимодействия), то это отражается и на "волнах возбуждения" или на соответствующих им "частицах возбуждения" — они также перестают быть независимыми, могут рассеиваться друг на друге, порождаться и исчезать. Изучение поля, т. о., можно свести к рассмотрению квантованных волн (или "частиц") возбуждений. Более того, никаких др. "частиц", кроме "частиц возбуждения", при данном методе описания не возникает, т.к. каждая частица-осциллятор отдельно в нарисованную общую картину квантованного осцилляторного поля не входит.
Рассмотренная "осцилляторная модель" поля имеет в основном иллюстративное значение (хотя, например, она довольно полно объясняет, почему в физике твердого тела методы К/b> являются эффективным инструментом теоретического исследования). Однако она не только отражает общие важные черты теории, но и позволяет понять возможность различных подходов к проблеме квантового описания полей.
Первый из описанных выше методов ближе к так называемой гейзенберговской картине (или представлению Гейзенберга) квантового поля. Второй — к "представлению взаимодействия", которое обладает преимуществом большей наглядности и поэтому, как правило, будет использоваться в дальнейшем изложении. При этом, конечно, будут рассматриваться различные физические поля, не имеющие механической природы, а не поле механических осцилляторов. Так, рассматривая электромагнитное поле, было бы неправильным искать за электромагнитными волнами какие-то механические колебания: в каждой точке пространства колеблются (т. е. изменяются во времени) напряженности электрического Е и Н полей. В гейзенберговской картине описания электромагнитного поля объектами теоретического исследования являются операторы (х) и 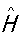 (х) (и др. операторы, которые через них выражаются), появляющиеся на месте классических величин. Во втором из рассмотренных методов на первый план выступает задача описания возбуждений электромагнитного поля. Если энергия "частицы возбуждения" равна E, а импульс р, то длина волны l и частота n соответствующей ей волны определяются формулами (1). Носитель этой порции энергии и импульса — квант свободного электромагнитного поля, или фотон. Т. о., рассмотрение свободного электромагнитного поля сводится к рассмотрению фотонов. (х) (и др. операторы, которые через них выражаются), появляющиеся на месте классических величин. Во втором из рассмотренных методов на первый план выступает задача описания возбуждений электромагнитного поля. Если энергия "частицы возбуждения" равна E, а импульс р, то длина волны l и частота n соответствующей ей волны определяются формулами (1). Носитель этой порции энергии и импульса — квант свободного электромагнитного поля, или фотон. Т. о., рассмотрение свободного электромагнитного поля сводится к рассмотрению фотонов.
Исторически квантовая теория электромагнитного поля начала развиваться первой и достигла известной завершенности; поэтому квантовой теории электромагнитных процессов — квантовой электродинамике — отводится в статье основное место. Однако, кроме электромагнитного поля, существуют и др. типы физических полей: мезонные поля различных типов, поля нейтрино и антинейтрино, нуклонные, гиперонные и т.д. Если физическое поле является свободным (т. е. не испытывающим никаких взаимодействий, в том числе и самовоздействия), то его можно рассматривать как совокупность невзаимодействующих квантов этого поля, которые часто просто называют частицами данного поля. При наличии взаимодействий (например, между физическими полями различных типов) независимость квантов утрачивается, а когда взаимодействия начинают играть доминирующую роль в динамике полей, утрачивается и плодотворность самого введения квантов этих полей (по крайней мере, для тех этапов процессов в этих полях, для которых нельзя пренебречь взаимодействием). Квантовая теория таких полей недостаточно разработана и в дальнейшем почти не обсуждается.
5. Ки релятивистская теория. Описание частиц высоких энергий должно проводиться в рамках релятивистской теории, т. е. в рамках специальной теории относительности Эйнштейна (см. Относительности теория). Эта теория, в частности, устанавливает важное соотношение между энергией E, импульсом р и массой m частицы;
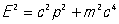 , (2) , (2)
(с — универсальная постоянная, равная скорости света в пустоте, с = 3×1010 см/сек). Из (2) видно, что энергия частицы не может быть меньше mc2. Энергия, конечно, не возникает "из ничего". Поэтому минимальная энергия, необходимая для образования частицы данной массы m (она называется массой покоя), равна mc2.
Если рассматривается система, состоящая из медленных частиц, то их энергия может оказаться недостаточной для образования новых частиц. В такой "нерелятивистской" системе число частиц может оставаться неизменным. Это и обеспечивает возможность применения для ее описания квантовой механики.
Все изложенное выше относится к порождению частиц, имеющих отличную от нуля массу покоя. Но у фотона, например, масса покоя равна нулю, так что для его образования совсем не требуется больших, релятивистских, энергий. Однако и здесь невозможно обойтись без релятивистской теории, что ясно хотя бы из того, что нерелятивистская теория применима лишь при скоростях, много меньших скорости света с, а фотон всегда движется со скоростью с.
Кроме необходимости рассматривать релятивистскую область энергий, есть еще одна причина важности теории относительности для К/b>: в физике элементарных частиц, изучение которых является одной из основных (и еще не решенных) задач К/b>, теория относительности играет фундаментальную роль. Это делает развитие релятивистской К/b> особенно важным.
Однако и нерелятивистская К/b> представляет значительный интерес хотя бы потому, что она успешно используется в физике твердого тела.
. Квантовая электродинамика
1. Квантованное свободное поле. Вакуумное состояние поля, или физический вакуум. Рассмотрим электромагнитное поле, или — в терминах квантовой теории — поле фотонов. Такое поле имеет запас энергии и может отдавать ее порциями. Уменьшение энергии поля на h n означает исчезновение одного фотона частоты n, или переход поля в состояние с уменьшившимся на единицу числом фотонов. В результате последовательности таких переходов в конечном итоге образуется состояние, в котором число фотонов равно нулю, и дальнейшая отдача энергии полем становится невозможной. Однако, с точки зрения К/b>, электромагнитное поле не перестает при этом существовать, оно лишь находится в состоянии с наименьшей возможной энергией. Поскольку в таком состоянии фотонов нет, его естественно назвать вакуумным состоянием электромагнитного поля, или фотонным вакуумом. Следовательно, вакуум электромагнитного поля — низшее энергетическое состояние этого поля.
Представление о вакууме как об одном из состояний поля, столь необычное с точки зрения классических понятий, является физически обоснованным. Электромагнитное поле в вакуумном состоянии не может быть поставщиком энергии, но из этого не следует, что вакуум вообще никак не может проявить себя. Физический вакуум — не "пустое место", а состояние с важными свойствами, которые проявляются в реальных физических процессах (см. ниже). Аналогично, и для др. частиц можно ввести представление о вакууме как о низшем энергетическом состоянии полей этих частиц. При рассмотрении взаимодействующих полей вакуумным называют низшее энергетическое состояние всей системы этих полей.
Если полю, находящемуся в вакуумном состоянии, сообщить достаточную энергию, то происходит возбуждение поля, т. е. рождение частицы — кванта этого поля. Т. о., появляется возможность описать порождение частиц как переход из "ненаблюдаемого" вакуумного состояния в состояние реальное. Такой подход позволяет перенести в К/b> хорошо разработанные методы квантовой механики — свести изменение числа частиц данного поля к квантовым переходам этих частиц из одних состояний в другие.
Взаимные превращения частиц, порождение одних и уничтожение других, можно количественно описывать при помощи так называемого метода вторичного квантования (предложенного в 1927 П. Дираком и получившего дальнейшее развитие в работах В. А. Фока (1932)).
2. Вторичное квантование. Переход от классической механики к квантовой называют просто квантованием, или реже — "первичным квантованием". Как уже говорилось, такое квантование не дает возможности описывать изменение числа частиц в системе. Основной чертой метода вторичного квантования является введение операторов, описывающих порождение и уничтожение частиц. Поясним действие этих операторов на простом примере (или модели) теории, в которой рассматриваются одинаковые частицы, находящиеся в одном и том же состоянии (например, все фотоны считаются имеющими одинаковую частоту, направление распространения и поляризацию). Т. к. число частиц в данном состоянии может быть произвольным, то этот случай соответствует бозе-частицам, или бозонам,
подчиняющимся Бозе — Эйнштейна статистике.
В квантовой теории состояние системы частиц описывается волновой функцией или вектором состояния. Введем для описания состояния с частицами вектор состояния ; квадрат модуля , ||2, определяющий вероятность обнаружения частиц, обращается, очевидно, в 1, если достоверно известно. Это означает, что вектор состояния с любым фиксированным нормирован на 1. Введем теперь оператор уничтожения частицы а– и оператор рождения частицы а+. По определению, а– переводит состояние с частицами в состояние с —1 частицей, т. е.
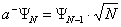 (3) (3)
Аналогично, оператор порождения частицы а+ переводит состояние в состояние с + 1 частицей:
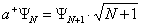 , (4) , (4)
(множители 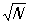 в (3) и в (3) и 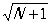 в (4) вводятся именно для выполнения условия нормировки: ||2= 1). В частности, при = 0 а+0 = 1, где 0 — вектор состояния, характеризующий вакуум; т. е. одночастичное состояние получается в результате порождения из "вакуума" одной частицы. Однако а–0 = 0, поскольку невозможно уничтожить частицу в состоянии, в котором частиц нет; это равенство можно считать определением вакуума. Вакуумное состояние 0 имеет в К/b> особое значение, т.к. из него при помощи операторов а+ можно получить любое состояние. Действительно, в рассматриваемом случае (когда состояние всей системы определяется только числом частиц) в (4) вводятся именно для выполнения условия нормировки: ||2= 1). В частности, при = 0 а+0 = 1, где 0 — вектор состояния, характеризующий вакуум; т. е. одночастичное состояние получается в результате порождения из "вакуума" одной частицы. Однако а–0 = 0, поскольку невозможно уничтожить частицу в состоянии, в котором частиц нет; это равенство можно считать определением вакуума. Вакуумное состояние 0 имеет в К/b> особое значение, т.к. из него при помощи операторов а+ можно получить любое состояние. Действительно, в рассматриваемом случае (когда состояние всей системы определяется только числом частиц)
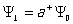 , ,
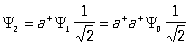 , (5) , (5)
……………………………………
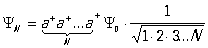
Легко показать, что порядок действия операторов а– и а+ не безразличен. Действительно, а–(а+0) = а–1 = 0, в то время как а+(а–0) = 0. Т. о., (a–a+ — a+a–)0 = 0, или
a–a+—a+a– = 1, (6)
т. е. операторы а+ и а– являются непереставимыми (некоммутирующими). Соотношения типа (6), устанавливающие связь между действием двух операторов, взятых в различном порядке называется перестановочными соотношениями, или коммутационными соотношениями для этих операторов, а выражения вида 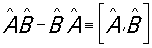 — коммутаторами операторов — коммутаторами операторов 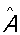 и и 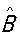 . .
Если учесть, что частицы могут находиться в различных состояниях, то, записывая операторы порождения и уничтожения, надо дополнительно указывать, к какому состоянию частицы эти операторы относятся. В квантовой теории состояния задаются набором квантовых чисел, определяющих энергию, спин и др. физические величины; для простоты обозначим всю совокупность квантовых чисел одним индексом n: так, а+n обозначает оператор рождения частицы в состоянии с набором квантовых чисел n. Средние числа частиц, находящихся в состояниях, соответствующих различным n, называются числами заполнения этих состояний.
Рассмотрим выражение a–n а+m0. Сначала на 0 действует "ближайший" к нему оператор а+m; это отвечает порождению частицы в состоянии m. Если n = m, то последующее действие оператора а–n приводит опять к 0, т. е. а–n а+n 0 = 0. Если n ¹ m, то а–n а+m 0 = 0, поскольку невозможно уничтожение таких частиц, которых нет (оператор а–n описывает уничтожение частиц в таких состояниях n, каких не возникает при действии a+n на 0). С учетом различных состоянии частиц перестановочные соотношения для операторов рождения и уничтожения имеют следующий вид:
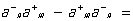 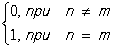
а–nа–m —а–m а–n = 0,
а+nа+m—а+m а+n = 0 (7)
Однако существуют поля, для которых связь между произведением операторов рождения и уничтожения, взятых в различном порядке, имеет др. вид: знак минус в (7) заменяется на плюс (это называется заменой коммутаторов на антикоммутаторы),
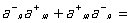 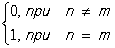 (8) (8)
а–nа–m —а–m а–n = 0, а+nа+m—а+m а+n = 0
(эти соотношения также относят к классу перестановочных соотношений, хотя они и не имеют вида (6)). Операторы, подчиняющиеся соотношениям (8), необходимо вводить для полей, кванты которых имеют полуцелый спин (т. е. являются фермионами) и вследствие этого подчиняются Паули принципу, согласно которому в системе таких частиц (например, электронов) невозможно существование двух или более частиц в одинаковых состояниях (в состояниях с одинаковым набором всех квантовых чисел). Действительно, построив вектор состояния, содержащего 2 частицы (двухчастичного состояния), а+m а+n 0, нетрудно убедиться (учитывая (8)), что при n = m он равен самому себе с обратным знаком; но это возможно только для величины, тождественно равной нулю. Т. о., если операторы рождения и уничтожения частиц удовлетворяют перестановочным соотношениям (8), то состояния с двумя (или более) частицами, имеющими одинаковые квантовые числа, автоматически исключаются. Такие частицы подчиняются Ферми — Дирака статистике. Для полей же, кванты которых имеют целый спин, операторы рождения и уничтожения частиц удовлетворяют соотношениям (7); здесь возможны состояния с произвольным числом частиц, имеющих одинаковые квантовые числа.
Наличие двух типов перестановочных соотношений имеет фундаментальное значение, поскольку оно определяет два возможных типа статистик.
Необходимость введения некоммутирующих операторов для описания систем с переменным числом частиц — типичная черта вторичного квантования.
Заметим, что "первичное квантование" также можно рассматривать как переход от классической механики, в которой координаты q и импульсы p являются обычными числами (т. е., конечно, qp = pq), к такой теории, в которой q и р заменяются некоммутирующими операторами: 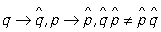 . Переход от классической теории поля к квантовой (например, в электродинамике) производится аналогичным методом, но только роль координат (и импульсов) должны при этом играть величины, описывающие распределение поля во всем пространстве и во все моменты времени. Так, в классической электродинамике поле определяется значениями напряженностей электрического Е и Н полей (как функций координат и времени). При переходе к квантовой теории Е и Н становятся операторами, которые не коммутируют с оператором числа фотонов в поле. . Переход от классической теории поля к квантовой (например, в электродинамике) производится аналогичным методом, но только роль координат (и импульсов) должны при этом играть величины, описывающие распределение поля во всем пространстве и во все моменты времени. Так, в классической электродинамике поле определяется значениями напряженностей электрического Е и Н полей (как функций координат и времени). При переходе к квантовой теории Е и Н становятся операторами, которые не коммутируют с оператором числа фотонов в поле.
В квантовой механике доказывается, что если 2 каких-либо оператора не коммутируют, то соответствующие им физические величины не могут одновременно иметь точные значения. Отсюда следует, что не существует такого состояния электромагнитного поля, в котором были бы одновременно точно определенными напряженности поля и число фотонов. Если, в силу физических условий, точно известно число фотонов, то совершенно неопределенными (способными принимать любые значения) оказываются напряженности полей. Если же известны точно эти напряженности, то неопределенным является число фотонов. Вытекающая отсюда невозможность одновременно положить равными нулю напряженности поля и число фотонов и является физической причиной того, что вакуумное состояние не представляет собой просто отсутствие поля, а сохраняет важные физические свойства.
3. Полевые методы в квантовой теории многих частиц. Математические методы К/b> (как уже отмечалось) находят применение при описании систем, состоящих из большого числа частиц: в физике твердого тела, ядра и т.д. Роль вакуумных состояний в твердом теле, например, играют низшие энергетические состояния, в которые система переходит при минимальной энергии (т. е. при температуре Т ® 0). Если сообщить системе энергию (например, повышая ее температуру), она перейдет в возбужденное состояние. При малых энергиях процесс возбуждения системы можно рассматривать как образование некоторых элементарных возбуждений — процесс, подобный порождению частиц в К/b> Отдельные элементарные возбуждения в твердом теле ведут себя подобно частицам — обладают определенной энергией, импульсом, спином. Они называются квазичастицами. Эволюцию системы можно представить как столкновение, рассеяние, уничтожение и порождение квазичастиц, что и открывает путь к широкому применению методов К/b> (см. Твердое тело). Одним из наиболее ярких примеров, показывающих плодотворность методов К/b> в изучении твердого тела является теория сверхпроводимости.
4. Кванты — переносчики взаимодействия. В классической электродинамике взаимодействие между зарядами (и токами) осуществляется через поле: заряд порождает поле и это поле действует на другие заряды. В квантовой теории взаимодействие поля и заряда выглядит как испускание и поглощение зарядом квантов Поля — фотонов. Взаимодействие же между зарядами, например между двумя электронами в К/b> является результатом их обмена фотонами: каждый из электронов испускает фотоны (кванты переносящего взаимодействие электромагнитного поля), которые затем поглощаются др. электроном. Это справедливо и для др. физических полей: взаимодействие в К/b> — результат обмена квантами поля.
В этой достаточно наглядной картине взаимодействия есть, однако, момент, нуждающийся в дополнительном анализе. Пока взаимодействие не началось, каждая из частиц является свободной, а свободная частица не может ни испускать, ни поглощать квантов. Действительно, рассмотрим свободную неподвижную частицу (если частица равномерно движется, всегда можно перейти к такой инерциальной системе отсчета, в которой она покоится). Запаса кинетической энергии у такой частицы нет, потенциальной — излучение энергетически невозможно. Несколько более сложные рассуждения убеждают и в неспособности свободной частицы поглощать кванты. Но если приведенные соображения справедливы, то, казалось бы, неизбежен вывод о невозможности появления взаимодействий в К/b>
Чтобы разрешить этот парадокс, нужно учесть, что рассматриваемые частицы являются квантовыми объектами и что для них существенны неопределенностей соотношения. Эти соотношения связывают неопределенности координаты частицы (Dх) и ее импульса (Dр):
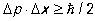 (9) (9)
Имеется и второе соотношение — для неопределенностей энергии DE и специфического времени Dt данного физического процесса (т. е. времени, в течение которого процесс протекает):
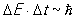 . (10) . (10)
Если рассматривается взаимодействие между частицами посредством обмена квантами поля (это поле часто называется промежуточным), то за Dt естественно принять продолжительность такого акта обмена. Вопрос о возможности испускания кванта свободной частицей отпадает: энергия частицы, согласно (10), не является точно определенной; при наличии же квантового разброса энергий DE законы сохранения энергии и импульса не препятствуют более ни испусканию, ни поглощению переносящих взаимодействие квантов, если только эти кванты имеют энергию ~ DE и существуют в течение промежутка времени 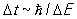 . .
Проведенные рассуждения не только устраняют указанный выше парадокс, но и позволяют получить важные физические выводы. Рассмотрим взаимодействие частиц в ядрах Ядра состоят из нуклонов, т. е. протонов и нейтронов. Экспериментально установлено, что вне пределов ядра, т. е. на расстояниях, больших примерно 10–12 см, взаимодействие неощутимо, хотя в пределах ядра оно заведомо велико. Это позволяет утверждать, что радиус действия ядерных сил имеет порядок L ~ 10–12 см. Именно такой путь пролетают, следовательно, кванты, переносящие взаимодействие между нуклонами в ядрах. Время пребывания квантов "в пути", даже если принять, что они движутся с максимально возможной скоростью (со скоростью света с), не может быть меньше, чем Dt "×L/c. Согласно предыдущему, квантовый разброс энергии DE взаимодействующих нуклонов получается равным DE ~ 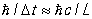 . В пределах этого разброса и должна лежать энергия кванта — переносчика взаимодействия. Энергия каждой частицы массы m складывается из ее энергии покоя, равной mc2, и кинетической энергии, растущей по мере увеличения импульса частицы. При не слишком быстром движении частиц кинетическая энергия мала по сравнению с mc2, так что можно принять DE " mc2. Тогда из предыдущей формулы следует, что квант, переносящий взаимодействия в ядре, должен иметь массу порядка . В пределах этого разброса и должна лежать энергия кванта — переносчика взаимодействия. Энергия каждой частицы массы m складывается из ее энергии покоя, равной mc2, и кинетической энергии, растущей по мере увеличения импульса частицы. При не слишком быстром движении частиц кинетическая энергия мала по сравнению с mc2, так что можно принять DE " mc2. Тогда из предыдущей формулы следует, что квант, переносящий взаимодействия в ядре, должен иметь массу порядка 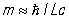 . Если подставить в эту формулу численные значения величин, то оказывается, что масса кванта ядерного поля примерно в 200—300 раз больше массы электрона. . Если подставить в эту формулу численные значения величин, то оказывается, что масса кванта ядерного поля примерно в 200—300 раз больше массы электрона.
Такое полукачественное рассмотрение привело в 1935 японского физика-теоретика Х. Юкава к предсказанию новой частицы; позже эксперимент подтвердил существование такой частицы, названной пи-мезоном. Этот блистательный результат значительно укрепил веру в правильность квантовых представлений о взаимодействии как об обмене квантами промежуточного поля, веру, сохраняющуюся в значительной степени до сих пор, несмотря на то, что количественную мезонную теорию ядерных сил построить все еще не удалось.
Если рассмотреть 2 настолько тяжелые частицы, что их можно считать классическими материальными точками, то взаимодействие между ними, возникающее в результате обмена квантами массы m, приводит к появлению потенциальной энергии взаимодействия частиц, равной
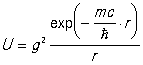 , (11) , (11)
где r — расстояние между частицами, a g — так называемая константа взаимодействия рассматриваемых частиц с полем квантов, переносящих взаимодействие (или иначе — заряд, соответствующий данному виду взаимодействия).
Если применить эту формулу к случаю, когда переносчиками взаимодействия являются кванты электромагнитного поля — фотоны, масса покоя которых m = 0, и учесть, что вместо g должен стоять электрический заряд е, то получится хорошо известная энергия кулоновского взаимодействия двух зарядов: эл = е2/r.
5. Графический метод описания процессов. Хотя в К/b> рассматриваются типично квантовые объекты, можно дать процессам взаимодействия и превращения частиц наглядные графические изображения. Такого рода графики впервые были введены американским физиком Р. Фейнманом и носят его имя. Графики, или диаграммы, Фейнмана, внешне похожи на изображение путей движения всех участвующих во взаимодействии частиц, если бы эти частицы были классическими (хотя ни о каком классическом описании не может быть и речи). Для изображения каждой свободной частицы вводят некоторую линию (которая, конечно, есть всего лишь графический символ распространения частицы): так, фотон изображают волнистой линией, электрон — сплошной. Иногда на линиях ставят стрелки, условно обозначающие "направление распространения" частицы. Ниже даны примеры таких диаграмм.
На рис. 1 изображена диаграмма, соответствующая рассеянию фотона на электроне: в начальном состоянии присутствуют один электрон и один фотон; в точке 1 они встречаются и происходит поглощение фотона электроном; в точке 2 появляется (испускается электроном) новый, конечный фотон. Это — одна из простейших диаграмм Комптон-эффекта.
Диаграмма на рис. 2 отражает обмен фотоном между двумя электронами: один электрон в точке 1 испускает фотон, который затем в точке 2 поглощается вторым электроном. Как уже говорилось, такого рода обмен приводит к появлению взаимодействия; т. о., данная диаграмма изображает элементарный акт электромагнитного взаимодействия двух электронов. Более сложные диаграммы, соответствующие такому взаимодействию, должны учитывать возможность обмена несколькими фотонами; одна из них изображена на рис. 3.
В приведенных примерах проявляется некоторое общее свойство диаграмм, описывающих взаимодействие между электронами и фотонами: все диаграммы составляются из простейших элементов — вершинных частей, или вершин, одна из которых (рис. 4) представляет испускание, а другая (рис. 5) — поглощение фотона электроном. Оба эти процесса в отдельности запрещены законами сохранения энергии и импульса. Однако если такая вершина входит как составная часть в некоторую более сложную диаграмму, как это было в рассмотренных примерах, то квантовая неопределенность энергии, возникающая из-за того, что на промежуточном этапе некоторая частица существует короткое время Dt, снимает энергетический запрет.
Частицы, которые рождаются, а затем поглощаются на промежуточных этапах процесса, называются виртуальными (в отличие от реальных частиц, существующих достаточно длительное время). На рис. 1 это — виртуальный электрон, возникающий в точке 1 и исчезающий в точке 2, на рис. 2 — виртуальный фотон и т.д. Часто говорят, что взаимодействие переносится виртуальными частицами. Можно несколько условно принять, что частица виртуальна, если квантовая неопределенность ее энергии DE порядка среднего значения энергии частицы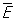 , и ее можно называть реальной, если DE << , и ее можно называть реальной, если DE << 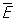 (для относительно медленно движущихся частиц с неравной нулю массой покоя m это условие сведется к неравенству DE << mc2). (для относительно медленно движущихся частиц с неравной нулю массой покоя m это условие сведется к неравенству DE << mc2).
Диаграммы Фейнмана не только дают наглядное изображение процессов, но и позволяют при помощи определенных математических правил вычислять вероятности этих процессов. Не останавливаясь детально на этих правилах, отметим, что в каждой вершине осуществляется элементарный акт взаимодействия, приводящий к превращению частиц (т. е. к уничтожению одних частиц и рождению других). Поэтому каждая из вершин дает вклад в амплитуду вероятности процесса, причем этот вклад пропорционален константе взаимодействия тех частиц (или полей), линии которых встречаются в вершине. Во всех приведенных выше диаграммах такой константой является электрический заряд е. Чем больше вершин содержит диаграмма процесса, тем в более высокой степени входит заряд в соответствующее выражение для амплитуды вероятности процесса. Так, амплитуда вероятности, соответствующая диаграммам 1 и 2 с двумя вершинами, квадратична по заряду (~ е2), а диаграмма 3 (содержащая 4 вершины) приводит к амплитуде, пропорциональной четвертой степени заряда (~ е4). Кроме того, в каждой вершине нужно учитывать законы сохранения (за исключением закона сохранения энергии — его применимость лимитируется квантовым соотношением неопределенностей для энергии и времени): импульса (отвечающий каждой вершине акт взаимодействия может произойти в любой точке пространства, т. е. неопределенность координаты Dх = ¥, и, следовательно, импульс определен точно), электрического заряда и т.д., а также вводить множители, зависящие от спинов частиц.
Выше были рассмотрены лишь простейшие виды диаграмм для некоторых процессов. Эти диаграммы не исчерпывают всех возможностей. Каждую из простейших диаграмм можно дополнить бесконечным числом все более усложняющихся диаграмм, включающих все большее число вершин. Например, приведенную на рис. 1 "низшую" диаграмму Комптон-эффекта можно усложнять, выбирая произвольно пары точек на электронных линиях и соединяя эти пары волнистой фотонной линией (рис. 6), т.к. число промежуточных (виртуальных) фотонных линий не лимитировано.
6. Взаимодействие частицы с вакуумом электромагнитного поля. Излучение На приведенных графиках взаимодействия двух электронов (рис. 2 и 3) каждый из фотонов порождается одним и поглощается др. электроном. Однако возможен и др. процесс (рис. 7): фотон, испущенный электроном в точке 1, через некоторое время поглощается им же в точке 2. Поскольку обмен квантами обусловливает взаимодействие, то такой график также является одной из простейших диаграмм взаимодействия, но только взаимодействия электрона с самим собой, или, что то же самое, с собственным полем. Этот процесс можно также назвать взаимодействием электрона с полем виртуальных фотонов, или с фотонным вакуумом (последнее название определяется тем, что реальных фотонов здесь нет). Т. о., собственное электромагнитное (электростатическое) поле электрона создается испусканием и поглощением (этим же электроном) фотонов. Такие взаимодействия электрона с вакуумом обусловливают экспериментально наблюдаемые эффекты (что свидетельствует о реальности вакуума). Самый значительный из этих эффектов — излучение фотонов Согласно квантовой механике, электроны в располагаются на квантовых энергетических уровнях, а излучение фотона происходит при переходе электрона с одного (высшего) уровня на другой, обладающий меньшей энергией. Однако квантовая механика оставляет открытым вопрос о причинах таких переходов, сопровождающихся так называемым спонтанным ("самопроизвольным") излучением; более того, каждый уровень выглядит здесь как вполне устойчивый. Физической причиной неустойчивости возбужденных уровней и спонтанных квантовых переходов, согласно К/b>, является взаимодействие с фотонным вакуумом. Образно говоря, взаимодействие с фотонным вакуумом трясет, раскачивает электрон — ведь при испускании и поглощении каждого виртуального фотона электрон испытывает толчок, отдачу; без этого электрон двигался бы устойчиво по орбите (ради наглядности, примем этот полуклассический образ). Один из таких толчков заставляет электрон "упасть" на более устойчивую, т. е. обладающую меньшей энергией, орбиту; при этом освобождается энергия, которая идет на возбуждение электромагнитного поля, т. е. на образование реального фотона.
То, что взаимодействие электронов с фотонным вакуумом обусловливает саму возможность переходов в (и в др. излучающих фотоны системах), а значит, и излучение, — это наибольший по масштабу и по значению эффект в квантовой электродинамике. Однако есть и другие, гораздо более слабые, "вакуумные эффекты", очень важные в принципиальном отношении; некоторые из них будут обсуждены в разделе .
7. Электронно-позитронный вакуум. В 1928 английский физик П. Дирак, решая задачу о релятивистском квантовом уравнении движения электрона, предсказал, что у электрона должен быть "двойник" — античастица, отличающаяся от электрона знаком электрического заряда. Такая частица, названная позитроном, вскоре была обнаружена экспериментально. Позитрон не может порождаться в одиночку — это исключается, например, законом сохранения электрического заряда. Электроны и позитроны могут появляться и исчезать (аннигилировать) лишь парами. Для рождения электронно-позитронной пары необходима достаточно большая энергия (не меньше удвоенной энергии покоя электрона), которую может поставить, например, "жесткий", т. е. имеющий большую энергию, фотон (гамма-квант), налетающий на какую-либо заряженную частицу. Однако рождение пары может происходить и виртуально. Тогда образовавшаяся пара, просуществовав очень недолгое время Dt, аннигилирует. Квантовый разброс энергий DE ~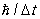 , если Dt очень мало, делает такой процесс энергетически разрешенным. , если Dt очень мало, делает такой процесс энергетически разрешенным.
Графически процесс рождения и аннигиляции виртуальной электронно-позитронной пары изображен на рис. 8: фотон в точке 1 исчезает, порождая пару, которая затем аннигилирует в точке 2, в результате чего вновь образуется фотон. (Позитрон изображается такой же сплошной линией, как и электрон, на которой условно стрелка направлена в противоположную сторону, т. е. "вспять" во времени.)
То обстоятельство, что электроны и позитроны не могут появляться и исчезать порознь, а возникают и уничтожаются только парами, показывает глубокое физическое единство электронно-позитронного поля. Электронное и позитронное поля выглядят как обособленные лишь до тех пор, пока не рассматриваются процессы, связанные с изменением числа электронов и позитронов.
Античастицы есть не только у электронов. Установлено, что каждая частица (кроме так назывемых истинно нейтральных частиц, например фотона и нейтрального пи-мезона) имеет свою античастицу. Процессы, подобные виртуальному рождению и аннигиляции электронно-позитронных пар, существуют для любых пар частица-античастица.
. Метод возмущений в квантовой теории поля
1. Математическая и физическая частица. Полевая масса. Перенормировка массы. Для описания взаимодействующих полей часто применяется следующий метод (который фактически уже был использован выше). Сначала рассматриваются кванты свободных полей (частицы). Это так называемое нулевое приближение, в котором взаимодействие вообще не учитывается. Затем в рассмотрение вводится взаимодействие — частицы перестают быть независимыми, появляется возможность их рассеяния, порождения и уничтожения в результате взаимодействия. Последовательное увеличение числа учитываемых процессов, обусловленных взаимодействием, математически достигается применением так называемого метода возмущений. Ввиду большой роли, которую играет этот метод в теории, обсудим его физический смысл подробнее. Процедура последовательного уточнения вклада от взаимодействий фактически применяется и в классической электродинамике. Поясним это на примере электрона и создаваемого им электромагнитного поля. Электрон выступает в теории как носитель определенной массы m0. Но так как он порождает электромагнитное поле, имеющее энергию Еэл, а следовательно (согласно релятивистскому соотношению E = mc2, и массу Еэл/c2, то, ускоряя электрон, нужно преодолевать и инерцию его электромагнитного (в простейшем случае — кулоновского) поля.
Т. о., вводя в рассмотрение взаимодействие между электроном и электромагнитным полем, к "неполевой", или "затравочной", массе m0 необходимо добавить "полевую" часть массы mпол = Еэл/c2. Вычисление полевой массы для точечной частицы (а именно такими приходится считать рассматриваемые в нулевом приближении "затравочные" частицы) приводит к лишенному физического смысла результату: mпол оказывается бесконечно большой. Действительно, энергия кулоновского поля частицы, имеющей заряд е и протяженность а, равна Екул = ke2/a (k — множитель порядка единицы, численное значение которого зависит от распределения заряда); переход к точечной частице (a ® 0) приводит Екул ® ¥.
Бесконечное значение (расходимость) полевой массы (хотя и в несколько измененном, "ослабленном" виде) сохраняется и при переходе от классической теории к квантовой. Больше того, появляются и расходимости др. типов. Анализ встречающихся здесь трудностей привел к появлению идеи так называемых перенормировок. Деление массы на полевую и неполевую возникает (как видно из предыдущего) из-за принятого метода рассмотрения: вначале вводится свободная "затравочная" частица, а затем "включается" взаимодействие. В эксперименте, конечно, нет ни "затравочной", ни полевой массы, там проявляется только общая масса частицы. В теории, что очень существенно, эти массы также выступают лишь в сумме, а не порознь, Объединение полевой и неполевой массы и использование для суммарной массы значения, получаемого не теоретически, а из опыта, называется перенормировкой массы.
Традиционный путь построения теории в рамках метода теории возмущений таков: вначале формулируется теория свободных (не взаимодействующих) частиц, а затем вводится в рассмотрение взаимодействие между ними. Так, например, сначала строится теория свободных электронов (или электронно-позитронного поля), а затем рассматривается взаимодействие этих "математических", или "голых", электронов с электромагнитным полем. Однако реально существующие в природе "физические" электроны, в отличие от "математических", всегда взаимодействуют с фотонами (хотя бы с виртуальными), и "выключить" это взаимодействие можно только умозрительно. Важной частью идеи перенормировок является указание на необходимость построения теории, в которой выступали бы не математические, а физические частицы.
Любопытно, что природа в какой-то мере дает возможность увидеть различие между частицей со "включенным" и "выключенным" электромагнитным взаимодействием. Например, известны три пи-мезона: с положительным (p+), отрицательным (p–) и нулевым (p°) электрическими зарядами. Это различные зарядовые состояния одной и той же частицы, Заряженные мезоны (p+ и p–) имеют большую массу, чем нейтральный (p°); очевидно, здесь проявляется добавка, обусловленная полевой (электромагнитной) массой, хотя теория пока не может достаточно четко объяснить этого явления количественно.
В К/b> процесс "облачения" математической частицы, т. е, ее превращение в физическую, выглядит сложнее, чем в классической электродинамике, где все сводится к "пристегиванию" к частице кулоновского "шлейфа". В квантовой теории физическая частица отличается от математической "шубой", гораздо более сложной по своему строению: ее образуют "облака" рождаемых и вслед затем поглощаемых частицей виртуальных квантов. Это могут быть кванты любого из полей, с которыми частица находится во взаимодействии (электромагнитного, электронно-позитронного, мезонного и т.д.). "Шуба" не есть нечто застывшее, — образующие ее кванты непрерывно порождаются и поглощаются. "Шуба" пульсирует, т. е. несущая ее частица как бы проводит часть времени в "облаченном", а часть — в "голом" состоянии. Какую именно часть — это определяется степенью интенсивности взаимодействий. Например, мезонные взаимодействия нуклонов более чем в сто раз интенсивнее электромагнитных; это позволяет предполагать, что мезонное "одеяние" протона более чем в сто раз "плотнее" электромагнитного. Это, может быть, позволяет понять, почему квантовая теория электромагнитных процессов даже при далеко не полном учете вакуумных эффектов блестяще согласуется с экспериментом, тогда как мезонная теория не добилась таких успехов. В квантовой электродинамике можно ограничиться рассмотрением процессов с малым числом виртуальных фотонов и виртуальных электроннопозитронных пар, что соответствует учету небольшого числа "низших" поправок по методу теории возмущений; в мезонной теории это не приводит к успеху, что и создает трудности, которые будут рассмотрены в разделе .
Все приведенные выше рассуждения о "шубе" частиц являются, строго говоря, полуинтуитивными и не могут быть пока переведены на язык точной теории. Однако они могут быть полезными хотя бы потому, что помогают уяснить отличие математической частицы от физической и понять, что описание последней является далеко не простой задачей.
2. Поляризация вакуума. Перенормировка заряда. Электрическое (и в первую очередь кулоновское) поле заряженной частицы оказывает влияние на распределение виртуальных электронно-позитронных пар (и пар любых других заряженных частиц-античастиц). Реальный электрон притягивает виртуальные позитроны и отталкивает виртуальные электроны. Это должно приводить к явлениям, напоминающим поляризацию среды, в которую вносится заряженная частица. Для описания таких явлений опять применим метод возмущений.
Поляризация электронно-позитронного вакуума (принято использовать подсказываемый приведенной аналогией термин) является чисто квантовым эффектом, вытекающим из К/b> Эта поляризация приводит к тому, что электрон оказывается окруженным плотным слоем позитронов из виртуальных пар, так что эффективный заряд электрона должен существенно изменяться. Возникает экранировка заряда, т. е. его эффективное уменьшение. Если рассматривать "затравочные" частицы как точечные, то экранировка оказывается полной, т. е. эффективный заряд нулевым (проблема "заряда нуль"). Для преодоления этой трудности используется идея перенормировки заряда. Здесь почти дословно повторяются приводившиеся при обсуждении перенормировки массы аргументы. Назовем "затравочным" заряд, который был бы у частицы, если бы исчезло взаимодействие с электронно-позитронным вакуумом (будем говорить только о нем, хотя, конечно, нужно учитывать и влияние виртуальных пар др. полей). Наличие такого взаимодействия приводит к появлению "поправки" к заряду. Корректно вычислять ее физики не умеют, как не умеют и определять "затравочный" заряд. Но поскольку эти две части заряда ни в эксперименте, ни в теории не выступают порознь, можно обойти трудность, подставляя на место общего заряда величину, непосредственно взятую из опыта. Эта процедура называется перенормировкой заряда. Перенормировки заряда и массы не решают проблем, возникающих в теории точечных частиц, они лишь изолируют эти проблемы на некотором этапе теории и (что весьма важно) дают возможность выделить конечные наблюдаемые части из бесконечных значений для некоторых величин, характеризующих физические частицы.
3. Некоторые наблюдаемые "вакуумные" эффекты. Существует возможность экспериментально наблюдать влияние"вакуума" на частицы. Оказывается, что "шуба" физических частиц зависит оттого, какие внешние поля действуют на эту частицу. Иначе говоря, полевые добавки к энергии частицы зависят от ее состояния. Общая полевая энергия, как уже говорилось, получается в теории точечных частиц бесконечно большой, но из этой бесконечно большой величины можно выделить конечную часть, которая меняется в зависимости от состояния частицы и поэтому может быть обнаружена на опыте.
Лэмбовский сдвиг уровня. В (и некоторых др. легких имеются два состоя |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|