
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Квантовая жидкость | Квантовая жидкость (далее К) жидкость, свойства которой определяются квантовыми эффектами. Примером К является жидкий при температуре, близкой к абсолютному нулю. Квантовые эффекты начинают проявляться в жидкости при достаточно низких температурах, когда длина волны де Бройля для частиц жидкости, вычисленная по энергии их теплового движения, становится сравнимой с расстоянием между ними. Для жидкого это условие выполняется при температуре 3-2 К.
Согласно представлениям классической механики, с понижением температуры кинетическая энергия частиц любого тела должна уменьшаться. В системе взаимодействующих частиц при достаточно низкой температуре последние будут совершать малые колебания около положений, соответствующих минимуму потенциальной энергии всего тела. При абсолютном нуле температуры колебания должны прекратиться, а частицы занять строго определенные положения, т. е. любое тело должно превратиться в Поэтому самый факт существования жидкостей вблизи абсолютного нуля температуры связан с квантовыми эффектами. В квантовой механике действует принцип: чем точнее фиксировано положение частицы, тем больше оказывается разброс значений ее скорости (см. Неопределенностей соотношение). Следовательно, даже при абсолютном нуле температуры частицы не могут занимать строго определенных положений, а их кинетическая энергия не обращается в нуль, остаются так называемые нулевые колебания. Амплитуда этих колебаний тем больше, чем слабее силы взаимодействия между частицами и меньше их масса. Если амплитуда нулевых колебаний сравнима со средним расстоянием между частицами тела, то такое тело может остаться жидким вплоть до абсолютного нуля температуры.
Из всех веществ при атмосферном давлении только два изотопа (4 и 3) имеют достаточно малую массу и настолько слабое взаимодействие между что остаются жидкими вблизи абсолютного нуля и позволяют тем самым изучить специфику К Свойствами К обладают также электроны в металлах.
К делятся на бозе-жидкости и согласно различию в свойствах частиц этих жидкостей и в соответствии с применяемыми для их описания статистиками Бозе - Эйнштейна и - Дирака (см. Статистическая физика). Бозе-жидкость известна только одна - жидкий 4, которого обладают равным нулю спином (внутренним моментом количества движения). более редкого изотопа 3 и электроны в металле имеют полуцелый спин (1/2), они образуют
Жидкий 4 был первой разносторонне исследованной К Теоретические представления, развитые для объяснения основных эффектов в жидком легли в основу общей теории К 4 при 2,171 К и давлении насыщенного пара испытывает фазовый переход рода в новое состояние Не со специфическими квантовыми свойствами. Само наличие точки перехода связывается с появлением так называемого бозе-конденсата (см. Бозе - Эйнштейна конденсация), т. е. конечной доли в состоянии с импульсом, строго равным нулю. Это новое состояние характеризуется сверхтекучестью, т. е. протеканием Не без всякого трения через узкие капилляры и щели. Сверхтекучесть была открыта П. Л. Капицей (1938) и объяснена Л. Д. Ландау (1941).
Согласно квантовой механике, любая система взаимодействующих частиц может находиться только в определенных квантовых состояниях, характерных для всей системы в целом. При этом энергия всей системы может меняться только определенными порциями - квантами. Подобно в котором энергия меняется путем испускания или поглощения светового кванта, в К изменение энергии происходит путем испускания или поглощения элементарных возбуждений, характеризующихся определенным импульсом р, энергией e(р), зависящей от импульса, и спином. Эти элементарные возбуждения относятся ко всей жидкости в целом, а не к отдельным частицам и называется в силу их свойств (наличия импульса, спина и т.д.) квазичастицами. Примером квазичастиц являются звуковые возбуждения в Не - фононы, с энергией 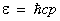 , где , где 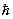 - Планка постоянная, деленная на 2p, с - скорость звука. Пока число квазичастиц мало, что соответствует низким температурам, их взаимодействие незначительно и можно считать, что они образуют идеальный газ квазичастиц. Рассмотрение свойств К на основе этих представлении оказывается, в известном смысле, более простым, чем свойств обычных жидкостей при высоких температурах, когда число возбуждений велико и их свойства не аналогичны свойствам идеального газа. - Планка постоянная, деленная на 2p, с - скорость звука. Пока число квазичастиц мало, что соответствует низким температурам, их взаимодействие незначительно и можно считать, что они образуют идеальный газ квазичастиц. Рассмотрение свойств К на основе этих представлении оказывается, в известном смысле, более простым, чем свойств обычных жидкостей при высоких температурах, когда число возбуждений велико и их свойства не аналогичны свойствам идеального газа.
Если К течет с некоторой скоростью u через узкую трубку или щель, то ее торможение за счет трения состоит в образовании квазичастиц с импульсом, направленным противоположно скорости течения. В результате торможения энергия К должна убывать, но не плавно, а определенными порциями. Для образования квазичастиц с требуемой энергией скорость потока должна быть не меньше, чем uc = min (e(p)/p); эту скорость называют критической. К, у которых uc ¹ 0, будут сверхтекучими, т.к. при скоростях, меньших uc, новые квазичастицы не образуются, и, следовательно, жидкость не тормозится. Предсказанный теорией Ландау и экспериментально подтвержденный энергетический спектр e(р) квазичастиц в Не удовлетворяет этому требованию.
Невозможность образования при течении с u < uc новых квазичастиц в Не приводит к своеобразной двухжидкостной гидродинамике. Совокупность имеющихся в Не квазичастиц рассеивается и тормозится стенками сосуда, она составляет как бы нормальную вязкую часть жидкости, в то время как остальная жидкость является сверхтекучей. Для сверхтекучей жидкости характерно появление в некоторых условиях (например, при вращении сосуда) вихрей с квантованной циркуляцией скорости сверхтекучей компоненты. В Не возможно распространение двух типов звука, из которых 1-й звук соответствует обычным адиабатическим колебаниям плотности, в то время как 2-й звук соответствует колебаниям плотности квазичастиц и, следовательно, температуры (см. Второй звук)
Наличие газа квазичастиц одинаково характерно как для бозе-, так и для В часть квазичастиц имеет полуцелый спин и подчиняется статистике - Дирака, это так назывемые одночастичные возбуждения. Наряду с ними в существуют квазичастицы с целочисленным спином, подчиняющиеся статистике Бозе - Эйнштейна, из них наиболее интересен "нуль-звук", предсказанный теоретически и открытый в жидком 3 (см. Нулевой звук). делятся на нормальные и сверхтекучие в зависимости от свойств спектра квазичастиц.
К нормальным относятся жидкий 3 и электроны в несверхпроводящих металлах, в которых энергия одночастичных возбуждений может быть сколь угодно малой при конечном значении импульса, что приводит к uc = 0. Теория нормальных была развита Л. Д. Ландау (1956-58).
Единственной, но очень важной сверхтекучей являются электроны в сверхпроводящих металлах (см. Сверхпроводимость). Теория сверхтекучей была развита Дж. Бардином, Л. Купером и Дж. Шриффером (1957) и Н. Н. Боголюбовым (1957). Между электронами в сверхпроводниках, согласно этой теории, преобладает притяжение, что приводит к образованию из электронов с противоположными, но равными по абсолютной величине импульсами связанных пар с суммарным моментом, равным нулю (см. Купера эффект). Для возникновения любого одночастичного возбуждения - разрыва связанной пары - необходимо затратить конечную энергию. Это приводит, в отличие от нормальных к uc ¹ 0, т. е. к сверхтекучести электронной жидкости (сверхпроводимости металла). Существует глубокая аналогия между сверхпроводимостью и сверхтекучестью. Как и в 4, в сверхпроводящих металлах имеется фазовый переход рода, связанный с появлением бозе-конденсата пар электронов. При определенных условиях в поле в так называемых сверхпроводниках рода появляются вихри с квантованным потоком, являющиеся аналогом вихрей в Не .
Кроме перечисленных выше К, к ним относятся смеси 3 и 4, которые при постепенном изменении соотношения компонентов образуют непрерывный переход от к бозе-жидкости. Согласно теоретическим представлениям, при чрезвычайно высоких давлениях и достаточно низких температурах все вещества должны переходить в состояние К, что возможно, например, в некоторых звездах.
Лит.: Ландау Л. Д. и Лифшиц Е. М., Статистическая физика, 2 изд., М., 1964; Абрикосов А. А., Халатников И. М., Теория "Успехи физических наук", 1958, т. 66, в. 2, с. 177; Физика низких температур, пер. с англ., М., 1959; Пайнс Д., Нозьер Ф., Теория квантовых жидкостей, пер. с англ., М., 1967.
С. В. Иорданский. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|