
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Квазичастицы | Квазичастицы (далее К) (от квази... и частицы), одно из фундаментальных понятий теории конденсированного состояния вещества, в частности теории твердого тела. Теоретическое описание и объяснение свойств конденсированных сред (твердых тел и жидкостей), исходящее из свойств составляющих их частиц ( молекул), представляет большие трудности, во-первых, потому, что число частиц огромно (~ 1022 частиц в 1 см3), и, во-вторых, потому, что они сильно взаимодействуют между собой. Из-за взаимодействия частиц полная энергия такой системы, определяющая многие ее свойства, не является суммой энергий отдельных частиц, как в случае идеального газа. Частицы конденсированной среды подчиняются законам квантовой механики; поэтому свойства совокупности частиц, составляющих твердое тело (или жидкость), могут быть поняты лишь на основе квантовых представлений. Развитие квантовой теории конденсированных сред привело к созданию специальных физических понятий, в частности к концепции К - элементарных возбуждений всей совокупности взаимодействующих частиц. Особенно плодотворные результаты концепция К дала в теории и жидкого гелия.
Свойства квазичастиц. Оказалось, что энергию E0 (или жидкого можно приближенно считать состоящей из двух частей: энергии основного (невозбужденного) состояния E0 (наименьшая энергия, соответствующая состоянию системы при абсолютном нуле температуры) и суммы энергий El элементарных (несводимых к более простым) движений (возбуждений):
E = E0 + 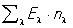
Индекс l характеризует тип элементарного возбуждения, nl - целые числа, показывающие число элементарных возбуждений типа l.
Т. о., энергию возбужденного состояния ( оказалось возможным записать так же, как и энергию идеального газа, в виде суммы энергий. Однако в случае газа суммируется энергия его частиц ( и молекул), а в случае суммируются энергии элементарных возбуждений всей совокупности (отсюда термин "К"). В случае газа, состоящего из свободных частиц, индекс l обозначает импульс р частицы, El - ее энергию El = p2/2m, m - масса частицы), nl - число частиц, обладающих импульсом р. Скорость u = p/m.
Элементарное возбуждение в также характеризуют вектором р, свойства которого похожи на импульс, его называют квазиимпульсом. Энергия El элементарного возбуждения зависит от квазиимпульса, но эта зависимость El(p) носит не такой простой характер, как в случае свободной частицы. Скорость распространения элементарного возбуждения также зависит от квазиимпульса и от вида функции El(p). В случае К индекс l включает в себя обозначение типа элементарного возбуждения, поскольку в конденсированной среде возможны элементарные возбуждения, разные по своей природе (аналог - газ, содержащий частицы различного сорта).
Введение для элементарных возбуждений термина "К" вызвано не только внешним сходством в описании энергии возбужденного состояния (или жидкого и идеального газа, но и глубокой аналогией между свойствами свободной (квантовомеханической) частицы и элементарным возбуждением совокупности взаимодействующих частиц, основанной на корпускулярно-волновом дуализме. Состояние свободной частицы в квантовой механике описывается монохроматической волной (см. Волны де Бройля), частота которой 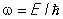 , а длина волны , а длина волны 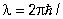 p (E и p (E и 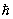 - энергия и импульс свободной частицы, - энергия и импульс свободной частицы, 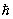 - Планка постоянная). В возбуждение одной из частиц (например, поглощение одним из фотона), приводящее из-за взаимодействия (связи) к возбуждению соседних частиц, не остается локализованным, а передается соседям и распространяется в виде волны возбуждений. Этой волне ставится в соответствие К с квазиимпульсом - Планка постоянная). В возбуждение одной из частиц (например, поглощение одним из фотона), приводящее из-за взаимодействия (связи) к возбуждению соседних частиц, не остается локализованным, а передается соседям и распространяется в виде волны возбуждений. Этой волне ставится в соответствие К с квазиимпульсом 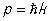 и энергией E = hw(k) (k - волновой вектор, длина волны l = 2p/k). и энергией E = hw(k) (k - волновой вектор, длина волны l = 2p/k).
Зависимость частоты от волнового вектора к позволяет установить зависимость энергии К от квазиимпульса. Эта зависимость El = E (p) называют законом дисперсии, является основной динамической характеристикой К, в частности определяет ее скорость 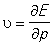 . Знание закона дисперсии К позволяет исследовать движение К во внешних полях, К, в отличие от обычной частицы, не характеризуется определенной массой, Однако, подчеркивая сходство К и частицы, иногда удобно вводить величину, имеющую размерность массы. Ее называют эффективной массой mэф. (как правило, эффективная масса зависит от квазиимпульса и от вида закона дисперсии). . Знание закона дисперсии К позволяет исследовать движение К во внешних полях, К, в отличие от обычной частицы, не характеризуется определенной массой, Однако, подчеркивая сходство К и частицы, иногда удобно вводить величину, имеющую размерность массы. Ее называют эффективной массой mэф. (как правило, эффективная масса зависит от квазиимпульса и от вида закона дисперсии).
Все сказанное позволяет рассматривать возбужденную конденсированную среду как газ К Сходство между газом частиц и газом К проявляется также в том, что для описания свойств газа К могут быть использованы понятия и методы кинетической теории газов, в частности говорят о столкновениях К (при которых имеют место специфические законы сохранения энергии и квазиимпульса), длине свободного пробега, времени свободного пробега и т.п. Для описания газа К может быть использовано кинетическое уравнение Больцмана. Одно из важных отличительных свойств газа К (по сравнению с газом обычных частиц) состоит в том, что К могут появляться и исчезать, т. е. число их не сохраняется. Число К зависит от температуры. При Т = 0 К квазичастицы отсутствуют. Для газа К как квантовой системы можно определить энергетический спектр (совокупность энергетических уровней) и рассматривать его как энергетический спектр или жидкого Разнообразие типов К велико, т.к. их характер зависит от структуры среды и взаимодействия между частицами. В одной и той же среде может существовать несколько типов К
К, как и обычные частицы, могут иметь собственный механический момент - спин. В соответствии с его величиной (выражаемой целым или полуцелым числом h) К можно разделить на бозоны и фермионы. Бозоны рождаются и исчезают поодиночке, рождаются и исчезают парами.
Для К- распределение по энергетическим уровням определяется функцией распределения для К-бозонов - функцией распределения Бозе. В энергетическом спектре (или жидкого который является совокупностью энергетических спектров всех возможных в них типов К, можно выделить и бозевскую "ветви". В некоторых случаях газ К может вести себя и как газ, подчиняющийся Больцмана статистике (например, газ электронов проводимости и дырок в невырожденном полупроводнике, см. ниже).
Теоретическое объяснение наблюдаемых макроскопических свойств (или жидкого основанное на концепции К, требует знания закона дисперсии К, а также вероятности столкновений К друг с другом и с дефектами в кристаллах. Получение численных значений этих характеристик возможно только путем применения вычислительной техники. Кроме того, существенное развитие получил полуэмпирический подход: количественные характеристики К определяются из сравнения теории с экспериментом, а затем служат для расчета характеристик (или жидкого
Для определения характеристик К используются рассеяние нейтронов, рассеяние и поглощение света, ферромагнитный резонанс и антиферромагнитный резонанс, ферроакустический резонанс, изучаются свойства металлов и полупроводников в сильных полях, в частности циклотронный резонанс, гальваномагнитные явления и т.д.
Концепция К применима только при сравнительно низких температурах (вблизи основного состояния), когда свойства газа К близки к свойствам идеального газа. С ростом числа К возрастает вероятность их столкновений, уменьшается время свободного пробега К и, согласно неопределенностей соотношению, увеличивается неопределенность энергии К Само понятие К теряет смысл. Поэтому ясно, что с помощью К нельзя описать все движения частиц в конденсированных средах. Например, К непригодны для описания самодиффузии (случайного блуждания по
Однако и при низких температурах с помощью К нельзя описать все возможные движения в конденсированной среде. Хотя, как правило, в элементарном возбуждении принимают участие все тела, оно микроскопично: энергия и импульс каждой К - масштаба, каждая К движется независимо от других. и электроны в конденсированной среде могут принимать участие в движении совершенно др. природы - макроскопическом по своей сути (гидродинамическом) и в то же время не теряющем своих квантовых свойств. Примеры таких движении: сверхтекучее движение в (см. Сверхтекучесть) и электрический ток в сверхпроводниках (см. Сверхпроводимость). Их отличительная черта - строгая согласованность (когерентность) движения отдельных частиц.
Представление о К получило применение не только в теории твердого тела и жидкого но и в др. областях физики: в теории ядра (см. Ядерные модели), в теории плазмы, в астрофизике и т.п.
Фононы. В совершают малые колебания, которые в виде волн распространяются по (см. Колебания кристаллической решетки). При низких температурах Т главную роль играют длинноволновые акустические колебания - обычные звуковые волны: они обладают наименьшей энергией. К, соответствующие волнам колебаний называют фононами. Фононы - бозоны; их число при низких температурах растет пропорционально T3. Это обстоятельство, связанное с линейной зависимостью энергии фонона ЕФ от его квазиимпульса р при достаточно малых квазиимпульсах ЕФ = sp, где s - скорость звука), объясняет тот факт, что теплоемкость (неметаллических) при низких температурах пропорциональна T3.
Фононы в сверхтекучем Основное состояние напоминает предельно вырожденный Бозе-газ. Как во всякой жидкости, в могут распространяться звуковые волны (волны колебаний плотности). Звуковые волны - единственный тип микроскопического движения возможного в вблизи основного состояния. Так как в звуковой волне частота w пропорциональна волновому вектору k: w = sk (s- скорость звука), то соответствующие К (фононы) имеют закон дисперсии E = sp. По мере увеличения импульса кривая E = E (p) отклоняется от линейного закона. Фононы также подчиняются статистике Бозе. Представление об энергетическом спектре как о фононном спектре не только описывает его термодинамические свойства (например, зависимость теплоемкости от температуры), но и объясняет явление сверхтекучести.
Магноны. В ферро- и антиферромагнетиках при Т = 0 К спины строго упорядочены. Состояние возбуждения системы связано с отклонением спина от "правильного" положения. Это отклонение не локализуется на определенном а переносится от к Элементарное возбуждение системы представляет собой волну поворотов спина (спиновая волна), а соответствующая ей К называют магноном. Магноны - бозоны. Энергия магнона квадратично зависит от квазиимпульса (в случае малых квазиимпульсов). Это находит отражение в тепловых и свойствах ферро- и антиферромагнетиков (например, при низких температурах отклонение ферромагнетика от насыщения ~ Т3/2). Высокочастотные свойства ферро- и антиферромагнетиков описываются в терминах "рождения" магнонов.
Экситон Френкеля представляет собой элементарное возбуждение электронной системы отдельного или молекулы, которое распространяется по в виде волны. Экситон, как правило, имеет весьма значительную (по масштабам) энергию ~ нескольких эв. Поэтому вклад экситонов в тепловые свойства твердых тел мал. Экситоны проявляют себя в оптических свойствах Обычно среднее число экситонов очень мало. Поэтому их можно описывать классической статистикой Больцмана.
Электроны проводимости и дырки. В твердых диэлектриках и полупроводниках наряду с экситонами существуют элементарные возбуждения, обусловленные процессами, аналогичными ионизации В результате такой "ионизации" возникают две независимо распространяющиеся К: электрон проводимости и дырка (недостаток электрона в Дырка ведет себя как положительно заряженная частица, хотя ее движение представляет собой волну электронной перезарядки, а не движение положительного иона. Электроны проводимости и дырки - Они являются носителями электрического тока в твердом теле. Полупроводники, у которых энергия "ионизации" мала, всегда содержат заметное количество электронов проводимости и дырок. Проводимость полупроводников падает с понижением температуры, т.к. число электронов и дырок при этом уменьшается.
Электрон и дырка, притягиваясь друг к другу, могут образовать экситон Мотта (квазиатом), который проявляет себя в оптических спектрах линиями поглощения (см. Экситон).
Поляроны. Взаимодействие электрона с колебаниями решетки приводит к ее поляризации вблизи электрона. Иногда взаимодействие электрона с решеткой настолько сильно, что движение электрона по сопровождается волной поляризации. Соответствующая К называется поляроном.
Электроны проводимости металла, взаимодействующие друг с другом и с полем ионов решетки, эквивалентны газу К со сложным законом дисперсии. Заряд каждой К равен заряду свободного электрона, а спин равен 1/2. Их динамические свойства, обусловленные законом дисперсии, существенно отличаются от свойств обычных свободных электронов. Электроны проводимости - В пространстве квазиимпульсов при Т = 0 К они заполняют область, ограниченную Ферми поверхностью. Возбуждение электронов проводимости означает появление пары: электрона "над" поверхностью и свободного места (дырки) "под" поверхностью. Электронный газ сильно вырожден не только при низких, но и при комнатных температурах (см. Вырожденный газ). Это обстоятельство определяет температурную зависимость большинства характеристик металла (в частности, линейную зависимость теплоемкости от температуры при Т ® 0).
Лит.: Ландау Л. Д., Лифшиц Е. М., Статистическая физика, 2 изд., М., 1964; Займан Дж., Принципы теории твердого тела, пер. с англ., М., 1966; Лифшиц И. М., К в современной физике, в сборнике: В глубь М., 1964; Рейф Ф., Сверхтекучесть и "К", в сборнике: Квантовая макрофизика, пер. с англ., М., 1967.
М. И. Каганов. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|