
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Евклида алгоритм | Евклида алгоритм (далее Е) способ нахождения наибольшего общего делителя двух целых чисел, двух многочленов или общей меры двух отрезков. Описан в геометрической форме в "Началах" Евклида. Для случая положительных чисел а и b, причем a ³ b, этот способ состоит в следующем. Деление с остатком числа а на число b всегда приводит к результату а = nb + b1, где частное n - целое положительное число, а остаток b1 - либо 0, либо положительное число, меньшее b (0 £ b1 < b). Будем производить последовательное деление:
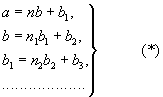
где все ni - положительные целые числа и 0 £ b1 < bi-1 до тех пор, пока не получится остаток, равный нулю. Этот последний остаток bk+1 можно не писать, так что ряд равенств (*) закончится так:
bk-2 = nk-1 + bk,
bk-1 = nkbk.
Последний положительный остаток bк в этом процессе и является наибольшим общим делителем чисел а и b. Е служит не только для нахождения наибольшего общего делителя, но и для доказательства его существования. В случае многочленов или отрезков поступают сходным образом. В случае несоизмеримых отрезков (см. Соизмеримые и несоизмеримые величины) Е оказывается бесконечным. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.10.2024 20:09:25
|

|

|
 |
|

|
 |
 |
 |
|