
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Динамическая система | Динамическая система (далее Д) (в классическом смысле), механическая система с конечным числом степеней свободы, например система конечного числа материальных точек или твердых тел, движущаяся по законам классической динамики. Состояние такой системы обычно характеризуется ее расположением (конфигурацией) и скоростью изменения последнего, а закон движения указывает, с какой скоростью изменяется состояние системы.
В простейших случаях состояние можно охарактеризовать посредством величин w1, ..., wm, которые могут принимать произвольные (вещественные) значения, причем двум различным наборам величин w1, ..., wm и w"1, ..., w"m отвечают различные состояния, и обратно, а близость всех wi к wi" означает близость соответствующих состояний системы. Закон движения тогда записывается в виде системы обыкновенных дифференциальных уравнений:
wi = fi(w1, ..., wm), i = 1, ..., m. (1)
Рассматривая значения w1, ..., wm как координаты точки w в m-мерном пространстве, можно геометрически представить соответствующее состояние Д посредством точки w. Эту точку называют фазовой (иногда также изображающей, или представляющей) точкой, а пространство - фазовым пространством системы (прилагательное "фазовый" связано с тем, что в прошлом состояния системы нередко называются ее фазами). Изменение состояния со временем изображается как движение фазовой точки по некоторой линии (так называемой фазовой траектории; часто ее называют просто траекторией) в фазовом пространстве. В последнем определено векторное поле, сопоставляющее каждой точке w выходящий из нее вектор f(w) с компонентами
(f1(w1, ..., wm), ..., fm(w1, ..., wm*(
Дифференциальные уравнения (1), которые с помощью введенных обозначений можно сокращенно записать в виде
w = f(w), (2)
означают, что в каждый момент времени векторная скорость движения фазовой точки равна вектору f(w), исходящему из той точки w фазового пространства, где в данный момент находится движущаяся фазовая точка. В этом состоит так называемая кинематическая интерпретация системы дифференциальных уравнений (1).
Например, состояние частицы без внутренних степеней свободы (материальной точки), движущейся в потенциальном поле с потенциалом (x1, x2, x3), характеризуется ее положением x = (x1, x2, x3) и скоростью x; вместо скорости можно использовать импульс p = mx, где m - масса частицы. Закон движения частицы можно записать в виде
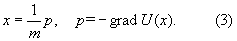
Формулы (3) представляют собой сокращенную запись системы шести обыкновенных дифференциальных уравнений 1-го порядка. Фазовым пространством здесь служит 6-мерное евклидово пространство, 6 компонент вектора фазовой скорости суть компоненты обычной скорости и силы, а проекция фазовой траектории на пространство положений частицы (параллельно пространству импульсов) есть траектория частицы в обычном смысле слова.
Термин "Д" применяется и в более широком смысле, означая произвольную физическую систему (например, систему автоматического регулирования, радиотехническую систему), описываемую дифференциальными уравнениями вида (1) или (2), и даже просто систему дифференциальных уравнений такого вида, безотносительно к ее происхождению. См. также ст. Эргодическая теория.
Лит.: Немыцкий В. В. и Степанов В. В., Качественная теория дифференциальных уравнений, 2 изд., М. - Л., 1949; Коддингтон Э. А., Левинсон Н., Теория обыкновенных дифференциальных уравнений, пер. с англ., М., 1958, гл. 13-17; Халмош П. ., Лекции по эргодической теории, пер. с англ., М., 1959; Лефшец С., Геометрическая теория дифференциальных уравнений, пер. с англ., М., 1961.
Д. В. Аносов.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|