
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Поверхности второго порядка | Поверхности второго порядка (далее П), поверхности, декартовы прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2-й степени:
a11x2 + a22y2 + a33z2 + 2a12xy + 2a23yz + 2a13xz + 2a14x + 2a24y + 2a34z + a44 = 0 (*)
Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую П В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из 17 приведенных ниже канонических видов, каждому из которых соответствует определенный класс П Среди них выделяют пять основных типов поверхностей. Именно,
1) эллипсоиды
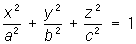 — эллипсоиды, — эллипсоиды,
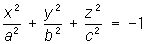 — мнимые эллипсоиды; — мнимые эллипсоиды;
2) гиперболоиды:
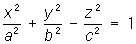 — однополостные гиперболоиды, — однополостные гиперболоиды,
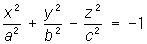 — двуполостные гиперболоиды; — двуполостные гиперболоиды;
3) параболоиды (p > 0, q > 0):
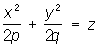 — эллиптические параболоиды, — эллиптические параболоиды,
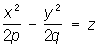 — гиперболические параболоиды; — гиперболические параболоиды;
4) конусы второго порядка:
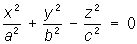 — конусы, — конусы,
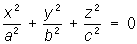 — мнимые конусы; — мнимые конусы;
5) цилиндры второго порядка:
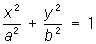 — эллиптические цилиндры, — эллиптические цилиндры,
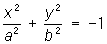 — мнимые эллиптические цилиндры, — мнимые эллиптические цилиндры,
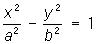 — гиперболические цилиндры, — гиперболические цилиндры,
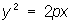 — параболические цилиндры. — параболические цилиндры.
Перечисленные П относятся к т. н. нераспадающимся П; распадающиеся П:
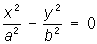 — пары пересекающихся плоскостей, — пары пересекающихся плоскостей,
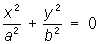 — пары мнимых пересекающихся плоскостей, — пары мнимых пересекающихся плоскостей,
х2 = а2 — пары параллельных плоскостей,
х2 = —а2 — пары мнимых параллельных плоскостей,
х2 = 0 — пары совпадающих плоскостей.
При исследовании общего уравнения П важное значение имеют т. н. основные инварианты — выражения, составленные из коэффициентов уравнения (*) и не меняющиеся при параллельном переносе и повороте системы координат. Например, если
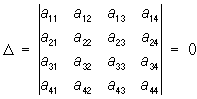 (aij = ajii), (aij = ajii),
то уравнение (*) определяет вырожденные П: конусы и цилиндры второго порядка и распадающиеся П; если определитель
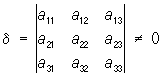 , ,
то поверхность имеет единственный центр симметрии (центр П) и называется центральной поверхностью. Если d = 0, то поверхность либо не имеет центра, либо имеет бесконечно много центров.
Для П установлена аффинная и проективная классификация. Две П считают принадлежащими одному аффинному классу, если они могут быть переведены друг в друга некоторым аффинным преобразованием (аналогично определяются проективные классы П). Каждому аффинному классу соответствует один из 17 канонических видов уравнения П Проективные преобразования позволяют установить связь между различными аффинными классами П Это объясняется тем, что при этих преобразованиях исчезает особая роль бесконечно удаленных элементов пространства. Например, эллипсоиды и двуполостные гиперболоиды, различные с аффинной точки зрения, принадлежат одному проективному классу П
Лит.: Александров П. С., Лекции по аналитической геометрии..., М., 1968; Ильин В. А., Позняк Э. Г., Аналитическая геометрия, 2 изд., М., 1971; Ефимов Н. В., Квадратичные формы и матрицы, 5 изд., М., 1972.
А. Б. Иванов.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 31.01.2026 03:02:37
|

|

|
 |
|

|
 |
 |
 |
|