
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Пирсона кривые | Пирсона кривые (далее П) семейство кривых распределения (т. е. кривых у = у (х), изображающих зависимость плотности распределения от х), удовлетворяющих дифференциальному уравнению
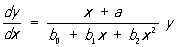 , ,
где a, bo, b1, b2— действительные числа. П классифицируются на 12 типов в зависимости от значения параметров а, b0, b1, b2 и интервала изменения х. Примерами П являются нормальное распределение, Стьюдента распределение, распределение c2.
Всякая П у (х) однозначно определяется заданием ее первых четырех моментов:
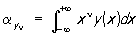 , n = 1, 2, 3, 4. , n = 1, 2, 3, 4.
На основании этого свойства П иногда используются в математической статистике для приближенного представления неизвестной плотности р (х). Пусть, например, имеется большой ряд независимых наблюдений x1, x2,..., xn случайной величины Х с неизвестной плотностью распределения р (х). Применяя метод моментов (см. Статистические оценки), полагают 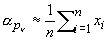 и для приближенного представления р (х) выбирают такую П y (x), для которой и для приближенного представления р (х) выбирают такую П y (x), для которой 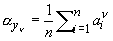 , где n = 1, 2, 3, 4. , где n = 1, 2, 3, 4.
П впервые были применены для построения эмпирических плотностей английским математиком К. Пирсоном в 1894.
Лит.: Кендалл М., Стьюарт А., Теория распределений, пер. с англ., М., 1966. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 15.02.2026 21:45:22
|

|

|
 |
|

|
 |
 |
 |
|