
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Многомерное пространство | Многомерное пространство (далее М)пространство, имеющее число измерений (размерность) более трех. Обычное евклидово пространство, изучаемое в элементарной геометрии, трехмерно; плоскости — двумерны, прямые — одномерны. Возникновение понятия Многомерное пространство связано с процессом обобщения самого предмета геометрии. В основе этого процесса лежит открытие отношений и форм, сходных с пространственными, для многочисленных классов математических объектов (зачастую не имеющих геометрического характера). В ходе этого процесса постепенно выкристаллизовалась идея абстрактного математического пространства как системы элементов любой природы, между которыми установлены отношения, сходные с теми или иными важными отношениями между точками обычного пространства. Наиболее общее выражение эта идея нашла в таких понятиях, как топологическое пространство и, в частности, метрическое пространство.
Простейшими Многомерное пространство являются n-мерные евклидовы пространства, где n может быть любым натуральным числом. Подобно тому, как положение точки обычного евклидова пространства определяется заданием трех ее прямоугольных координат, "точка" n-мерного евклидова пространства задается n "координатами" x1, x2, ..., xn (которые могут принимать любые действительные значения); расстояние r между двумя точками M(x1, x2, ..., xn) и М"(у1, y2, ..., yn) определяется формулой
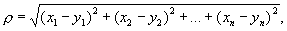
аналогичной формуле расстояния между двумя точками обычного евклидова пространства. С сохранением такой же аналогии обобщаются на случай n-мерного пространства и другие геометрические понятия. Так, в Многомерное пространство рассматриваются не только двумерные плоскости, но и k-мерные плоскости (k < n), которые, как и в обычном евклидовом пространстве, определяются линейными уравнениями (или системами таких уравнений).
Понятие n-мерного евклидова пространства имеет важные применения в теории функций многих переменных, позволяя трактовать функцию n переменных как функцию точки этого пространства и тем самым применять геометрические представления и методы к изучению функций любого числа переменных (а не только одного, двух или трех). Это и было главным стимулом к оформлению понятия n-мерного евклидова пространства.
Важную роль играют и другие Многомерное пространство Так, при изложении физического принципа относительности пользуются четырехмерным пространством, элементами которого являются т. н. "мировые точки". При этом в понятии "мировой точки" (в отличие от точки обычного пространства) объединяется определенное положение в пространстве с определенным положением во времени (поэтому "мировые точки" и задаются четырьмя координатами вместо трех). Квадратом "расстояния" между "мировыми точками" М`(х`, y`, z`, t`) и М"(х", y", z", t") (где первые три "координаты" — пространственные, а четвертая — временная) естественно считать здесь выражение
(M` M")2 = (x` - x")2 + (y` — y")2 + (z` — z")2 — c2(t` — t")2,
где с — скорость света. Отрицательность последнего члена делает это пространство "псевдоевклидовым".
Вообще n-мерным пространством называется топологическое пространство, которое в каждой своей точке имеет размерность n. В наиболее важных случаях это означает, что каждая точка обладает окрестностью, гомеоморфной открытому шару n-мерного евклидова пространства.
Подробнее о развитии понятия Многомерное пространство, геометрии Многомерное пространство, а также лит. см. в ст. Геометрия.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 31.01.2026 12:08:44
|

|

|
 |
|

|
 |
 |
 |
|