|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Гравитационное поле Земли | Гравитационное поле Земли (далее Г)поле силы тяжести; силовое поле, обусловленное притяжением (тяготением) Земли и центробежной силой, вызванной ее суточным вращением. Зависит также (незначительно) от притяжения Луны, Солнца и др. небесных тел и масс земной атмосферы. Гравитационное поле Земли характеризуется силой тяжести (см. Гравиметрия), потенциалом силы тяжести и различными производными от него. Потенциал имеет размерность см2.сек–2. За единицу измерения первых производных потенциала, в том числе силы тяжести, в гравиметрии принимается миллигал (мгл), равный 10–3 см.сек–2, а вторых производных - этвеш (Е), равный 10–9 сек–2. Часть потенциала силы тяжести, обусловленная только притяжением масс Земли, называется потенциалом земного притяжения, или геопотенциалом.
Для решения практических задач потенциал земного притяжения представляется в виде ряда
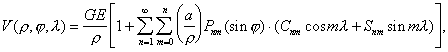
где r - геоцентрическое расстояние; j и l - географическая широта и долгота точки, в которой рассматривается потенциал; nm - присоединенные функции Лежандра; GE - произведение постоянной тяготения на массу Земли, равное 398 603·109 м3 сек–2, а - большая полуось Земли; nm и nm - безразмерные коэффициенты, зависящие от фигуры Земли и внутреннего распределения масс в ней. Главный член ряда - 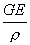 соответствует потенциалу притяжения шара с массой Земли. Второй по величине член (содержащий 20) учитывает сжатие Земли. Последующие члены, коэффициенты которых на три порядка и более меньше, чем 20, отражают детали фигуры и строения Земли. Из-за отсутствия точных данных об истинном распределении масс внутри Земли и о ее фигуре невозможно непосредственно вычислить коэффициенты nm и nm. Поэтому они определяются косвенно по совокупности измерений силы тяжести на поверхности Земли и по наблюдениям возмущений в движении близких искусственных спутников Земли (ИСЗ). В табл. приведены результаты определения коэффициентов разложения, установленные на основе наблюдений движения ИСЗ. Аналогичными рядами описывается поле силы тяжести Земли.
Для удобства решения различных задач Г. и. З. условно разделяется на нормальную и аномальную части. Основная - нормальная часть, описываемая несколькими первыми членами разложения, соответствует идеализированной Земле ("нормальной" Земле) простой геометрической формы и с простым распределением плотности внутри нее. Аномальная часть поля меньше по величине, но имеет сложное строение. Она отражает детали фигуры и распределения плотности реальной Земли. Нормальная часть поля силы тяжести рассчитывается по формулам распределения ускорения нормальной силы тяжести g. В СССР и др. социалистических странах наиболее часто используется формула Гельмерта (1901-09):
g = 978030 (1 + 0,005302 sin2j - -0,000007sin 22j) мгл.
Формула Кассиниса (1930), называемая международной, имеет вид:
g = 978049 (1 + 0,0052884 sin2j - 0,0000059 sin2 2j) мгл.
Существуют другие, менее распространенные, формулы, учитывающие небольшое долготное изменение g, а также асимметрию Северного и Южного полушарий. Ведется подготовка к переходу к единой новой формуле с учетом уточненного абсолютного значения силы тяжести. С помощью формул распределения нормальной силы тяжести, зная высоты пунктов наблюдений, а также строение окружающего рельефа и плотности слагающих его пород, вычисляют аномалии силы тяжести, которые применяются для решения большинства задач гравиметрии.
Потенциал силы тяжести используется при изучении фигуры Земли, близкой к уровенной поверхности Гравитационное поле Земли, а также в астродинамике при изучении движения искусственных спутников в Гравитационное поле Земли (уровенной называется поверхность, во всех точках которой потенциал имеет одинаковое значение; сила тяжести направлена к ней по нормали). Одна из уровенных поверхностей, которая совпадает с невозмущенной средней поверхностью океанов, называется геоидом. По направлению силы тяжести устанавливается отвес и определяется положение астрономического зенита. Поскольку уклонения отвеса приближенно равны отношению горизонтальной составляющей притяжения к силе тяжести, то знание их величин в определенном смысле позволяет судить и о Гравитационное поле Земли
Вторые производные потенциала силы тяжести применяются при решении геологоразведочных и геодезических задач. Вертикальный градиент силы тяжести, соответствующий нормальной части Гравитационное поле Земли, от полюса к экватору изменяется всего на 0,1% от его полной величины, равной в среднем для всей Земли 3086 этвеш. Намного меньше по абсолютной величине нормальные горизонтальные градиенты силы тяжести и вторые производные потенциала силы тяжести, характеризующие кривизну уровенной поверхности Земли. Аномальная часть вторых производных потенциала позволяет судить о плотностных неоднородностях в верхних частях земной коры. По величине она достигает в равнинных местах десятков, а в горных - сотен этвеш. В гравиметрической разведке, помимо вторых производных потенциала силы тяжести, используются третьи производные потенциала, получаемые путем пересчета по аномалиям силы тяжести. Сила тяжести измеряется гравиметрами и маятниковыми приборами, а вторые производные потенциала силы тяжести - гравитационными вариометрами.
Коэффициенты (умноженные на 10°) разложения потенциала земного притяжения в ряд по сферическим функциям, определенные по наблюдениям движения искусственных спутников Земли (по данным Смитсоновской астрофизической обсерватории, США, опубл. 1970)
m
|
0
|
1
|
2
|
3
|
4
|
5
|
С2m
|
-1082,63
|
-
|
2,41
|
-
|
-
|
-
|
2m
|
-
|
-
|
-1,36
|
-
|
-
|
-
|
3m
|
2,54
|
1,97
|
0,89
|
0,69
|
-
|
-
|
3m
|
-
|
0,26
|
-0,63
|
1,43
|
-
|
-
|
4m
|
1,59
|
-0,53
|
0,33
|
0,99
|
-0,08
|
-
|
4m
|
-
|
-0,49
|
0,71
|
-0,15
|
0,34
|
-
|
4m
|
0,23
|
-0,05
|
0,61
|
-0,43
|
-0,27
|
0,13
|
5m
|
-
|
-0,10
|
-0,35
|
-0,09
|
0,08
|
-0,60
|
Лит.: Жонголович И., Внешнее гравитационное поле Земли и фундаментальные постоянные, связанные с ним, "Тр. института теоретической астрономии", 1952, в. 3; Бровар В. В., В. А., Шимбирев Б. П., Теория фигуры Земли, М., 1961; Грушинский Н. П., Теория фигуры Земли, М., 1963.
М. У. Сагитов, В. А. Кузиванов.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 31.10.2025 21:19:16
|
|
|
|
|
|
|
|
|
|
|
